
Barney Come Home!
By Paulo Tan
Suppose Barney is in a triangular region ABC. If Barney starts at point D and travels on a parallel path to line AF, then he will end up on line AB at point E (fig1). The dashed red line represents Barney’s path. He then travels parallel to line BC and ends up on line AC at point F. If Barney continues this geometric travel process will he ever come home to point D?
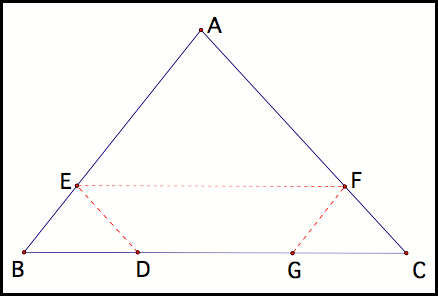
Fig1
We’ll start by analyzing the path that Barney has traveled so far (fig2). Notice that Barney’s path form two parallelograms, BEFG and DEFC.
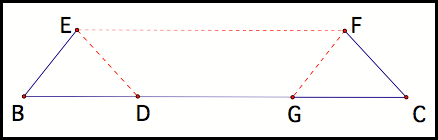
Fig2
Triangle EBD appears to be
congruent to triangle FGC. Let’s
try to prove it:
Since
opposite sides and angles of parallelograms are congruent then from
parallelogram BEFG:
Š
Angle EBD is congruent
to angle GFE
Š
Line segment BE is
congruent to line segment GF
From
parallelogram DEFC:
Š
Angle FCG is congruent
to angle DEF
Š
Line segment FC is
congruent to line segment ED
In
addition, since line EF is parallel to line BC, then:
Š
Angle DEF is congruent
to angle EDB
Š
Angle GFE is congruent
to angle FGC
By the transitive property:
Š
Angle EBD is congruent
to angle FGC
Š
Angle FCG is congruent
to angle EDB
It follows
that the third angle of each triangle must be congruent: angle BED is congruent
to angle GFC. Thus, by the Side
Angle Side Postulate triangle EBD is congruent to triangle FGC.
The next two paths result in
Barney landing on point H on side AB and then on to point I on side AC (fig3).
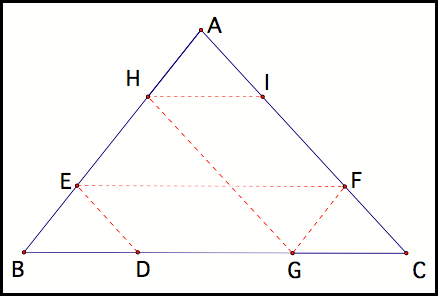
Fig 3
Once again, notice that there
are two new sets of parallelograms that are formed: parallelograms GHAF and
HICG (fig4).
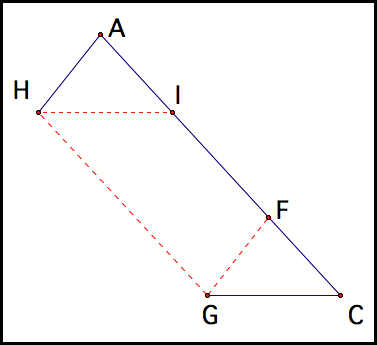
Fig 4
Earlier we proved that
triangles FGC and EBD are congruent.
Using a similar proof we could show that triangle FGC is congruent to
triangle AHI. As a result we have
that triangles EBD, FGC, and AHI are congruent to one another.
We could think of Barney’s
path in terms of modular arithmetic.
Š
The first, fourth,
seventh, tenth, … paths are all parallel to side AC.
Š
The second, fifth,
eighth, eleventh, … paths are all parallel to side BC.
Š
The third, sixth, ninth,
twelfth, … paths are all parallel to side AB.
Figure 5 shows Barney’s path in
terms of the different equivalence classes (shown in different colors) in
modulo three. Notice that the
sixth path takes Barney from point I back home to point D.
By using modular arithmetic
we know that the sixth path must be parallel to side AB. In addition, we have shown that
triangles EBD, AHI, and FGC are all congruent. Therefore, if Barney’s sixth path did not intersect at point
D, then we would have a contradiction of the proven facts.
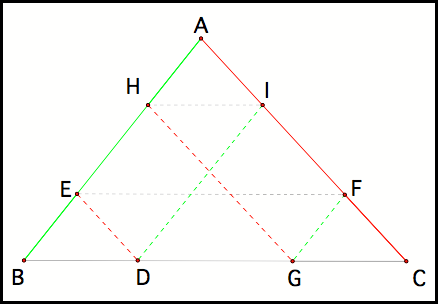
Fig 5
The result of Barney’s parallel path is that congruent triangles will be formed. Thus, we could conclude that Barney’s journey inside the triangular region will take at most six paths before he returns home no matter where he starts.
Click HERE
for a GSP file to see Barney’s path from different starting points on line
segment BC.
The GSP file confirms that
Barney’s journey will six paths for all of the starting points on side BC
except for the endpoints and a particular point on side BC that only seems to
only require Barney to take three paths before returning home (fig 6).
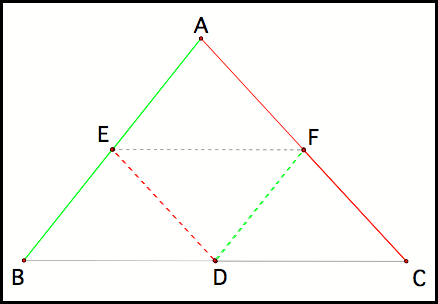
Fig 6
In figure 6, points D, E, and
F appear to be the midpoints of their respective sides. Lets prove this.
We know:
§
Line AB is parallel to
line DF
§
Line BC is parallel to
line EF
§
Line AC is parallel to
line DE
Thus
using the Alternate Interior and Corresponding angle theorem we conclude that:
§
Angle a’s are congruent to each other (fig 7)
§
Angle b’s are congruent to each other
§
Angle c’s are congruent to each other
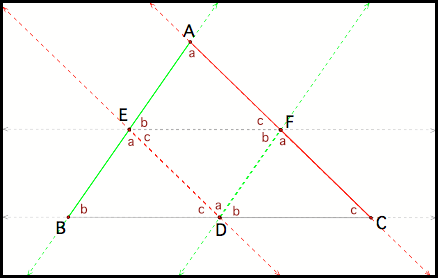
Fig 7
Therefore
triangles AEF, EBD, FDC, DFE are all similar to one another. In addition, AEF, EBD, FDC, DFE are all
similar to ABC. It follows that:
Š
Line segment BC is twice
the length of line segment EF
Š
Line segment AB is twice
the length of line segment DF
Š
Line segment AC is twice
the length of line segment DE
Thus
by the Mid-segment Theorem we have, D, E, and F as the midpoints of their
respective sides.
Hence, if Barney starts at
the midpoint then he only has three paths to take before he comes home. At any other point, besides the
endpoints, Barney must take six paths before coming home.
Next, let’s see what happens
when Barney starts his journey outside of triangle ABC (fig8). Click HERE
for a GSP file to see Barney’s path from outside of triangle ABC.
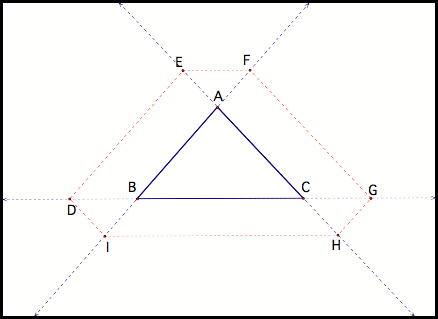
Fig 8
We see that Barney will still
take six paths before returning home.
Suppose that Barney was in a regular
pentagonal region (fig 9). If
Barney takes his parallel paths as he did with the triangle will he ever return
home?
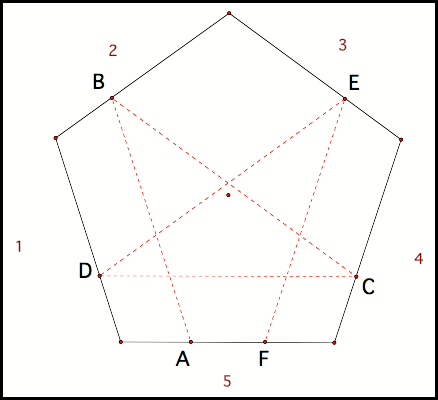
Fig 9
We could see that in this case we will need to use modulo five. This will be very useful in reducing the confusion caused by so many more lines that will be involved in this case. We need to establish the order of lines that Barney will travel parallel to. In a triangle there are only two choices. In a pentagon there are four. In this case, Barney will start on side 5. He will first travel parallel to side 1, then side 3, then side 5, then side 2, and side 4.
As expected, we see that after five paths, Barney returns to the starting side.
Repeating the process, we see
that Barney, as when he was in the triangle, returns home after two cycles (fig
10).
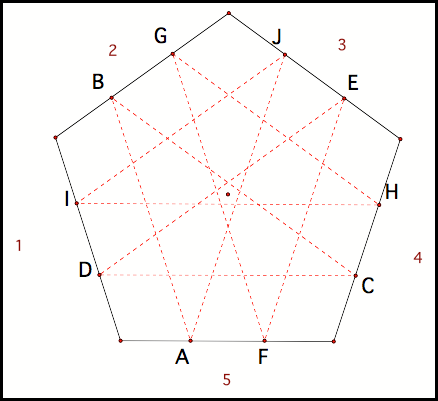
Fig 10
When Barney travel’s inside the regular pentagon, his path leaves behind some congruent quadrilaterals (fig 11).
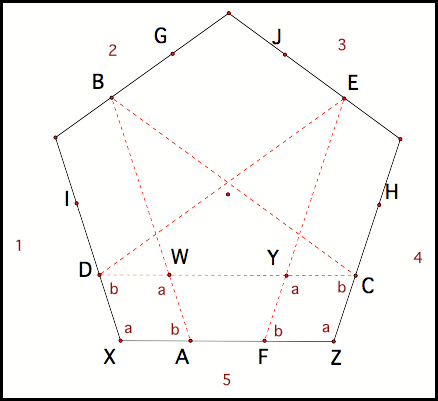
Fig 11
We see that quadrilaterals DWAX and CYFZ congruent to because:
Š Quadrilaterals DWAX and CYFZ are parallelograms since opposite sides are parallel.
Š Since we represents a regular polygon, then base angles are congruent.
Š Opposite sides of parallelograms are congruent.
As Barney travels around the pentagon other congruent quadrilaterals are formed (fig 12). Just like we proved quadrilaterals DWAX and CYFZ are congruent we could similarly show that all these “corner” quadrilaterals are congruent to one another. Thus, as with the triangle, Barney must return home, otherwise there will be contradiction of the proven congruencies.
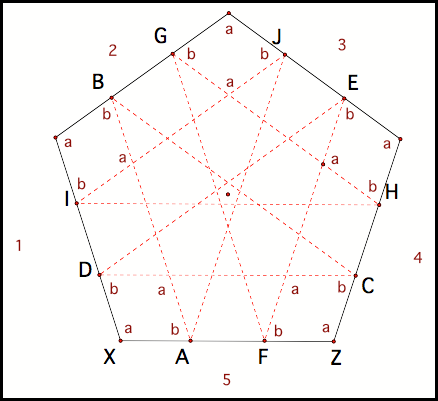
Fig 12
What if Barney’s starting point is the midpoint? Just as in the triangle Barney’s journey is cut to just one cycle (fig 13).
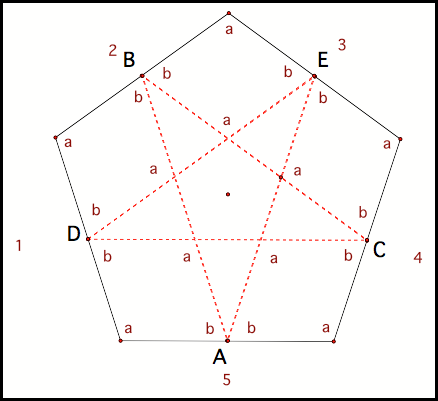
Fig 13
What if the region is not a regular polygon (fig14)?
Fig 14
Fig 14b
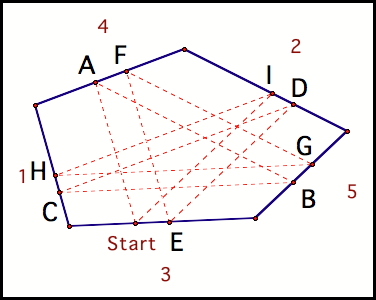
Fig 14c
GSP suggests that Barney will
make it home in a polygon (14c).
However, the quadrilaterals that his path makes are not congruent since
the polygon is not regular.
Can Barney make it back home
in five paths? Figure 15 shows
there exists a starting point where it appears Barney will be able to take five
paths to get back home.
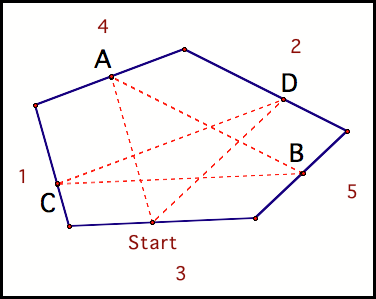
Fig 15
How about a regular heptagon (fig 16)?
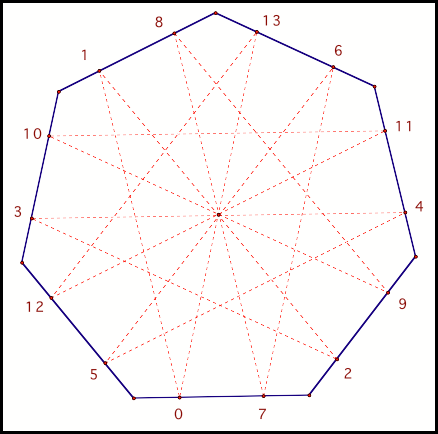
Fig 16
Notice again we have what
appear to be congruent “corner” quadrilaterals. We should be able to prove using similar techniques as we
did with the triangle and the regular pentagon.
We should expect similar
results with the midpoint as the starting point (fig 17).
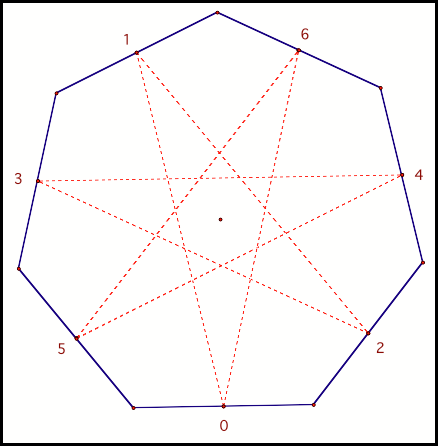
Fig 17
Thus, it appears that any odd
nth-gon will help Barney return home.
It remains to show that
Barney could return home in a region with an even number of sides, although it
seems unlikely.