
All About Ceva
By Paulo Tan
Suppose that we have a
triangle ABC with an arbitrary point P inside. Draw lines from each vertex through point P and extend to
find the point of intersection at the feet (fig 1). With the help of GSP, notice that (AF)(BD)(EC) =
(FB)(DC)(EA) for any location of P inside the triangle. Click HERE to
explore different locations of point P.
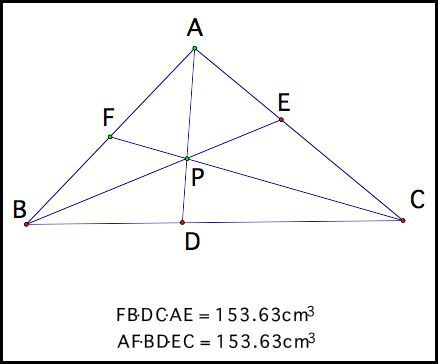
Fig 1
LetÕs see why (AF)(BD)(EC) = (FB)(DC)(EA). First start by drawing line j through point B and parallel to line AC. Now extend lines AD and CF. Mark the point of intersection from lines AD and CF to line j (fig 2)
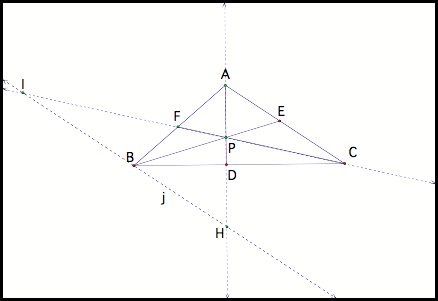
Fig 2
Notice that angle BDH is
congruent to angle ADC since they are vertical angles. Also, angles DBH and DCA are alternate
interior angles, thus congruent.
Hence, triangle BDH is similar to triangle CDA (fig 3).
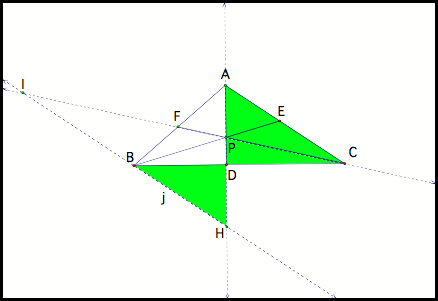
Fig 3
By the similar argument we see that triangle IPB is similar to triangle CPE (fig 4); triangle HPB is similar to triangle APE (fig 4b); triangle IBF is similar to triangle CAF (fig 4c).
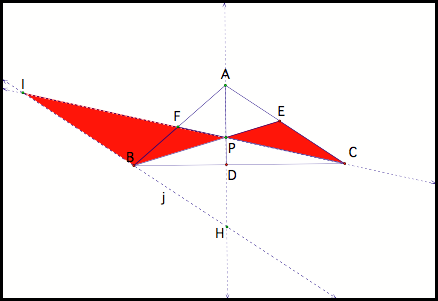
Fig 4
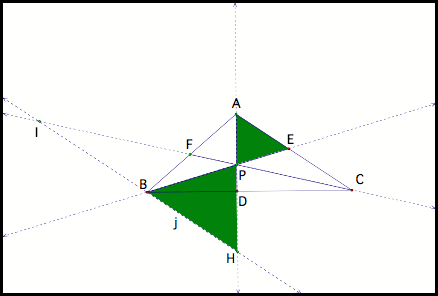
Fig 4b
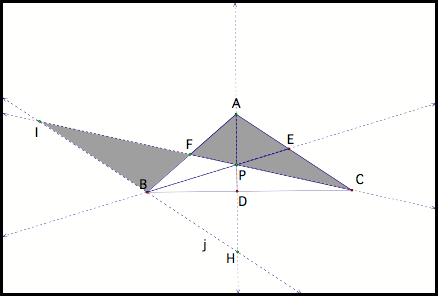
Fig 4c
So we have four pairs of
similar triangles:
1) BDH and CDA
2) IPB and CPE
3) HPB and APE
4) IBF and CAF
We could now use properties of
similar triangle and some algebra to show that (AF)(BD)(CE) = (BF)(CD)(AE)


WeÕll start with triangle ABC
with point P inside. Suppose we
have line AD and line BE intersect at point P (fig 5).
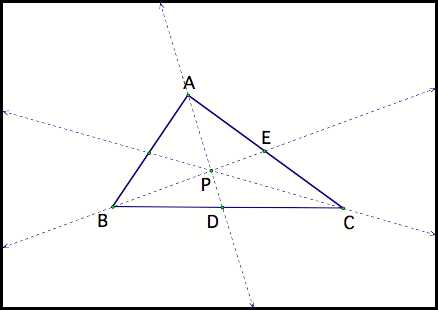
Fig 5
Now suppose line CP
intersects segment AB at some point X (fig 6).
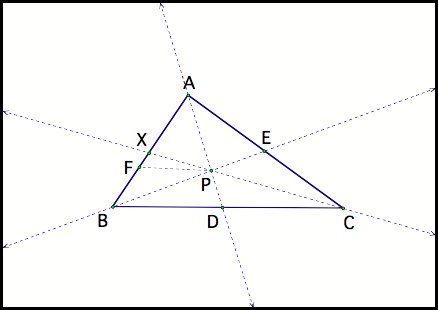
Fig 6


Next letÕs use CevaÕs Theorem
to show that the Centroid is a point of concurrency.
By definition a line AD bisects
segment BC, line BE bisects segment AC, and line CF bisects line AB (fig 7)
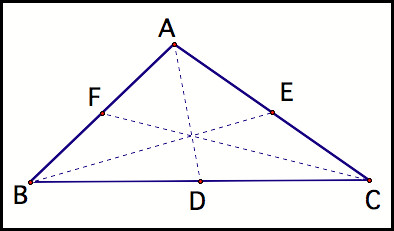
Fig 7
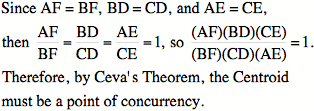
Next, weÕll use CevaÕs
Theorem to show that the Orthocenter is a point of concurrency. We know line AD is the altitude of line
BC, line BE is the altitude of line AC, and CF is the altitude of line AB (fig
8).
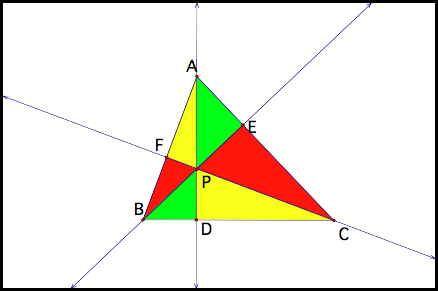
Fig 8
By the Angle-Angle-Angle Theorem we note that:
á Triangle AFP is similar to triangle CDP
á Triangle BFP is similar to triangle CEP
á Triangle BDP is similar to triangle AEP

Now lets show that the
Incenter is a point of concurrency.
We have the angle bisectors of each angle. Start with triangle ABC and the angle bisector of angle B
(fig 9).
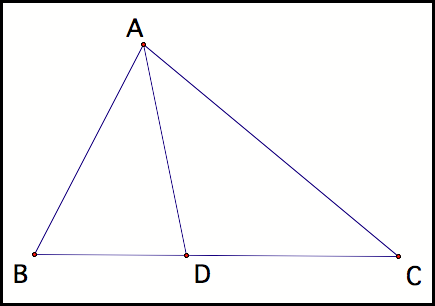
Fig 9

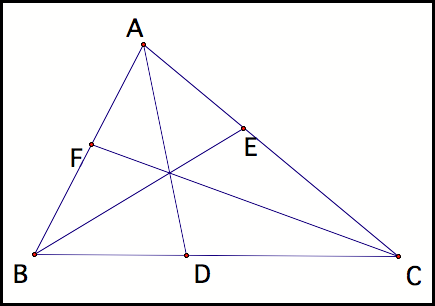
Fig 10

All the work weÕve done so
far has dealt with point P on the inside of the triangle. Click HERE to
for a GSP file to explore what happens when point P is on the outside.
According to GSP we see that
CevaÕs Theorem holds when point P is outside the triangle.