Polar Coordinates

A Presentation for Pre Calculus Students

By Paulo Tan

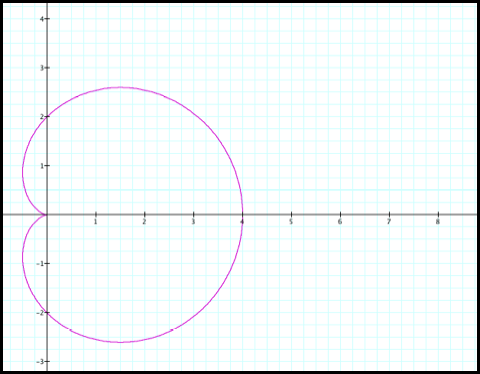
Here is our first example: Sketch the graph of r = 2+2cosq. We’ll start by graphing in the rectangular coordinate (fig1). We’ll use the graph in the rectangular coordinate to help us graph in the polar coordinate.

(Note: Some browsers may display pheta as q. Depending on the browser you’re using the rotation angle may either be pheta or q)

Case 1: r = 2+2cosq

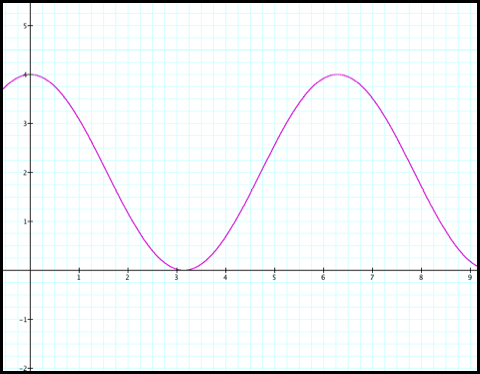
Fig1

1) Notice that r decreases from 4 to 2 as q increases from 0 to pi/2. So plotting this in polar coordinate gives us:

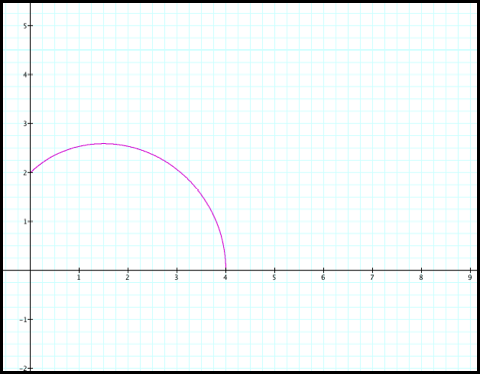
2) Next, r decreases from 2 to 0 as q increases from pi/2 to pi.

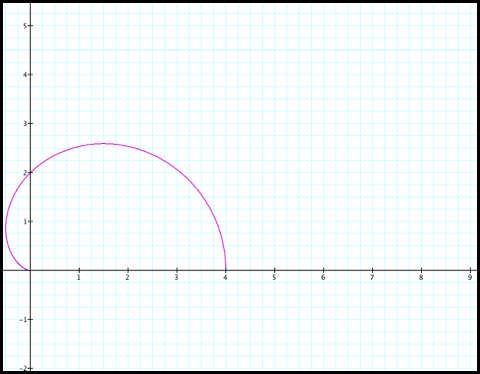
3) r increases from 0 to 2 as q increases from pi to 3pi/2:

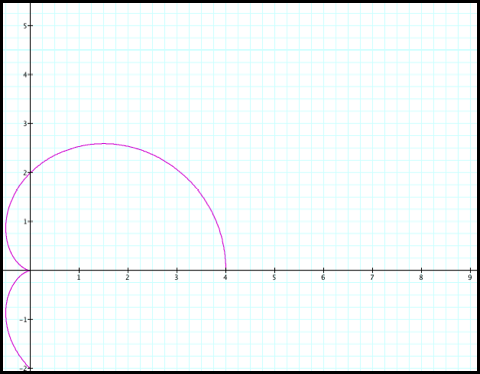
4) r increases from 2 to 4 as q increase from 3pi/2 to 2pi:

Next, lets sketch the graph of r = 2+2cos(3q).

Again to help us construct this equation in polar coordinates we’ll use the graph in the rectangular coordinate plane (fig2).

Case 2: r = 2+2cos(3q)

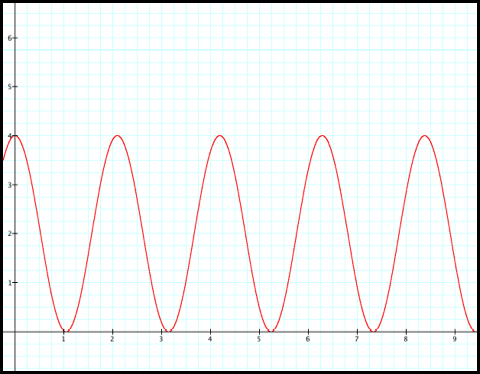
Fig2.

As expected, the graph in case two completes three full cycles for q values of 0 to 2pi.

1) Notice that r decreases from 4 to 2 as q increases from 0 to pi/6. So plotting this in polar coordinate gives us:

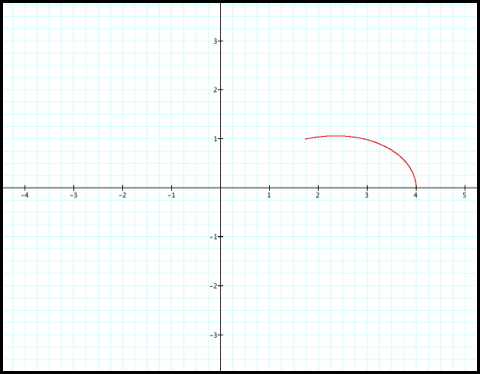
2) Next, r decreases from 2 to 0 as q increases from pi/6 to pi/3:

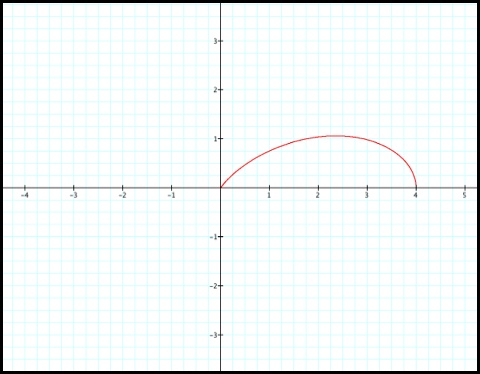
3) r increases from 0 to 2 as q increases from pi/3 to pi/2:

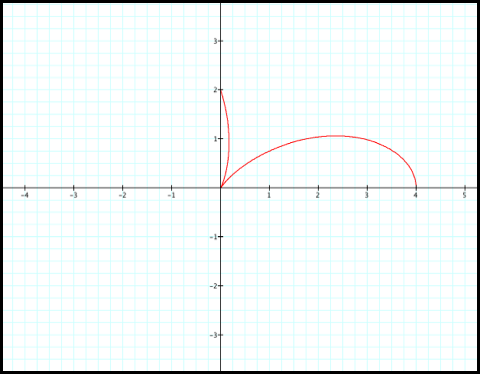
4) r increases from 2 to 4 as q increase from pi/2 to 2pi/3:

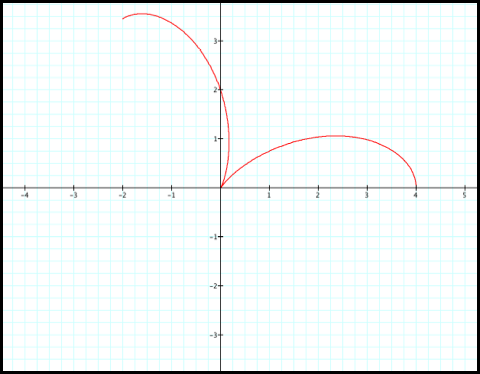
5) r decreases from 4 to 2 as q increases from 2pi/9 to 5pi/6:

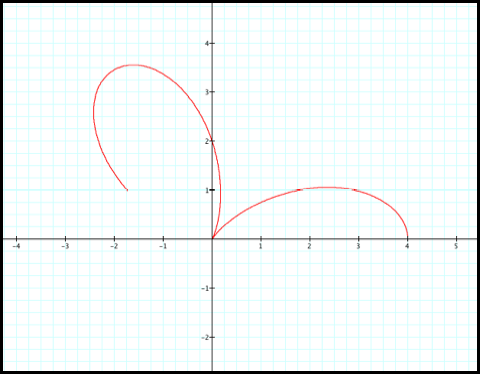
6) r decreases from 2 to 0 as q increases from 5pi/6 to pi:

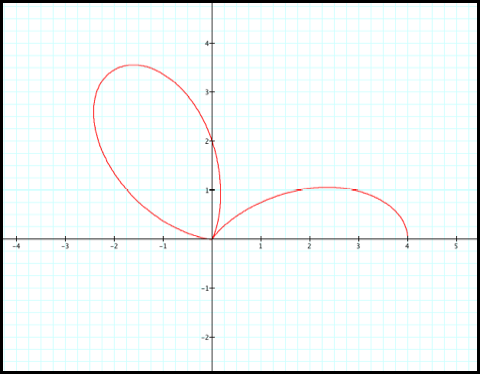
7) r increases from 0 to 2 as q increases from pi to 7pi/6:

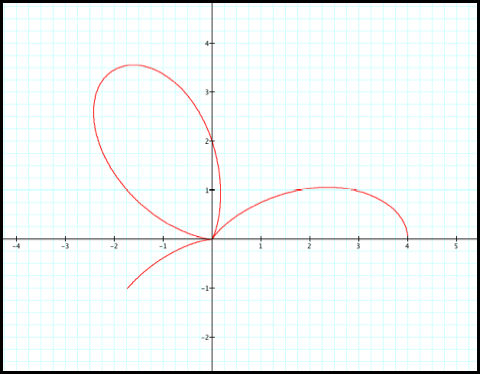
8) r increases from 2 to 4 as q increases from 7pi/6 to 4pi/3:

9) r decreases from 4 to 2 as q increases from 4pi/3 to 3pi/2:

10) r decreases from 2 to 0 as q increases from 3pi/2 to 5pi/3:

11) r increases from 0 to 2 as q increases from 5pi/3 to 11pi/6:

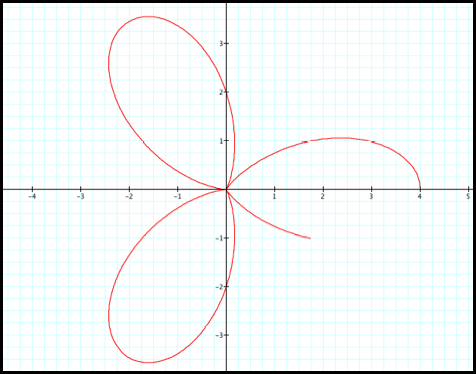
12) r increases from 2 to 4 as q increases from 11pi/6 to 2pi:

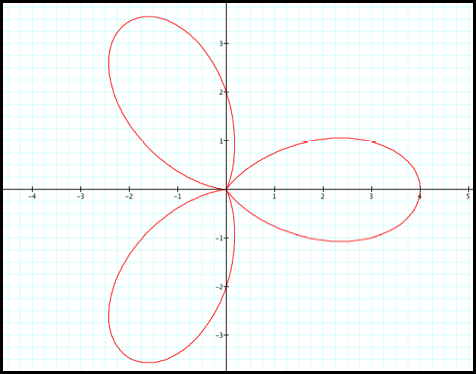
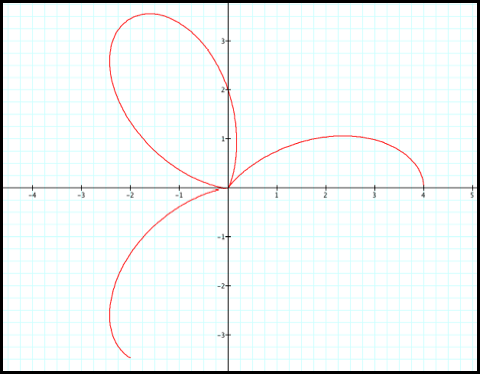
What do you think the graph of r = 2 + 2cos(5q) will look like? As you probably predicted (fig3), since you know the equation shows five cycles.

Case 3: r = 2 + 2cos(5q)

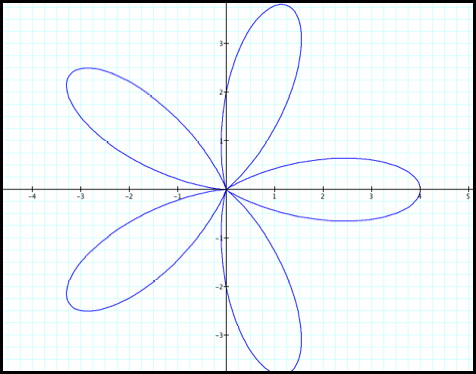
Fig3.

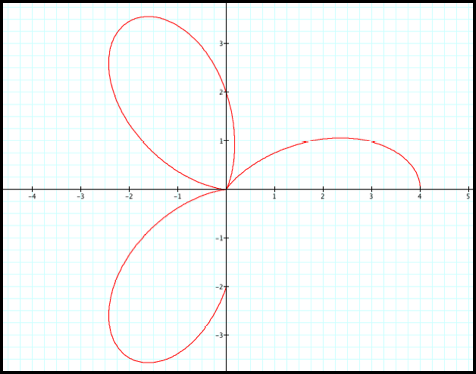
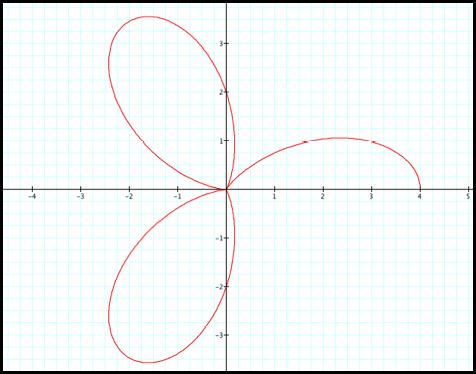
We should then expect similar results for the even multipliers of q (fig 4, 5, and 6).

Case 4: r = 2 + 2cos(2q)

Case 5: r = 2 + 2cos(4q)

Case 6: r = 2 + 2cos(8q)

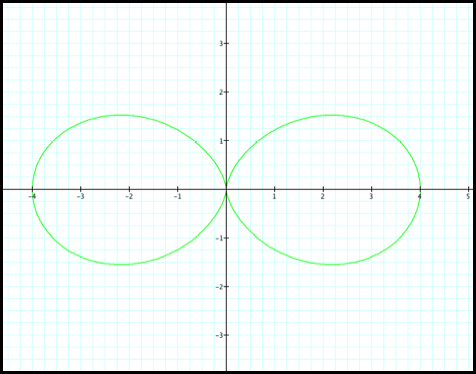
Fig4.

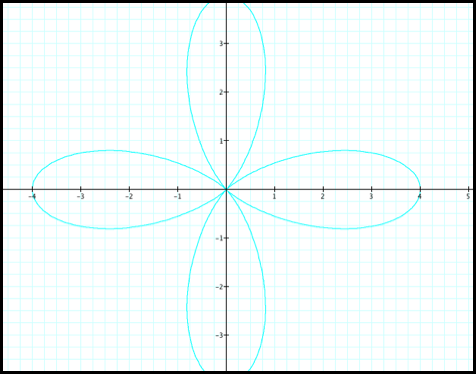
Fig5.

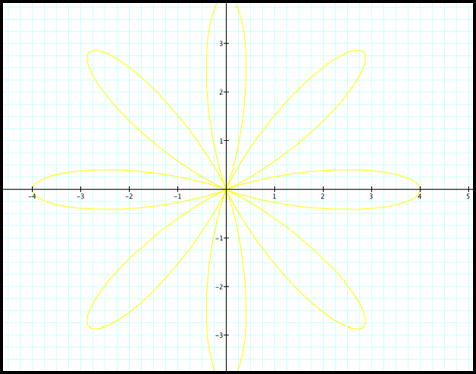
Fig6

The examples we investigated so far has focused on the equation of form

r = a +bcos(kq), where a=b=2. Let's try some other values for a and b (fig7). Since the period is the same in all three equations, it should keep its base shape. However, the different “shrink/stretch” changes the size of the graph.

Case 7: r = -1-1cos(2q), r = 2 + 2cos(2q), and r= 3 + 3cos(2q)

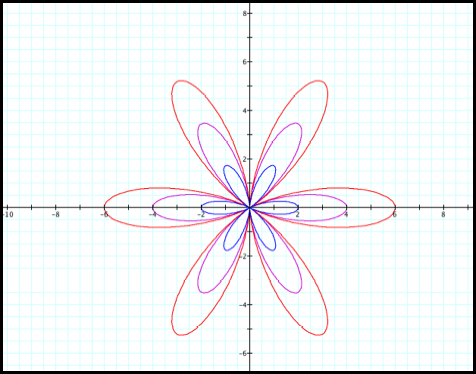
Fig 7

Lets see what happen when the a and b values are different but with k =1.

Case 8: r = -1 + 2 cos(q)

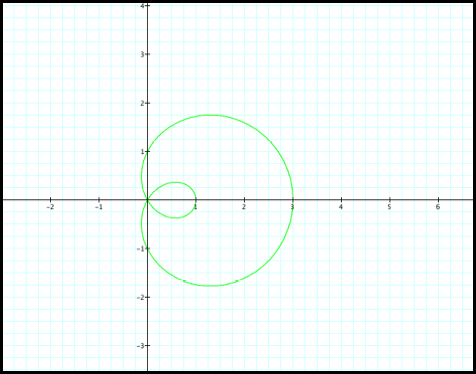
Fig8.

We see that the graph is very similar to the one in Case 1. Lets again refer to the rectangular coordinate to help us along. We notice the only change in the equation from Case 1 to Case 8 is the a value. Recall that the a value shifts the graph up/down. Thus the graph for Case 8 in the rectangular coordinate should come as no surprise:

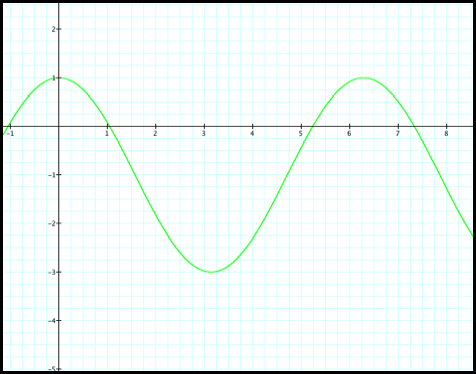
You notice that we will encounter negative r values.

1) According to the rectangular graph of Case 8, it looks the polar graph starts at r=1 and decreases to 0, as q increases from 0 to pi/3.

2) r decreases from 0 to -1, as q increases from pi/3 to pi/2

Here we have our first negative r value. Negative r values takes on the point which is on the straight line directly opposite from the positive r value (fig8b). In other words the points with negative r values would be on the opposite quadrants as the points with positive r values. Another way to think about it is as a reflection about the origin.

The purple curve represents r increasing from 0 to 1, as q increases from pi/3 to pi/2. The purple curve is the familiar curve we’ve encountered so far with positive r values. On the other hand, the graph of Case 8 (green curve), represents r decreasing from 0 to -1, as q increases from pi/3 to pi/2.

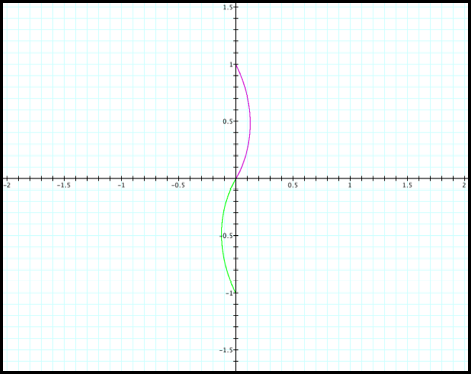
Fig8b.

3) r decreases from -1 to -3, as q increases from pi/2 to pi. We are still working with negative r values. So by looking at the purple curve (fig8c) we could operate a reflection about the origin to obtain the graph of Case 8 for the interval pi/2 to pi.

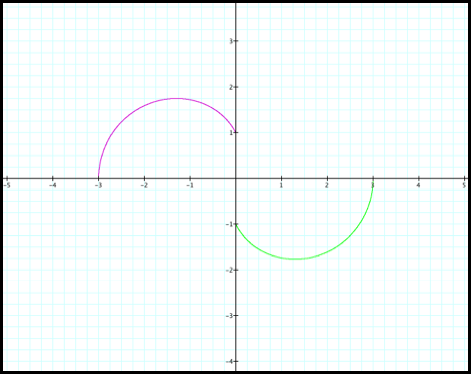
Fig 8c.

4) r increases from -3 to -1, as q increases from pi to 3pi/2 (fig8d).

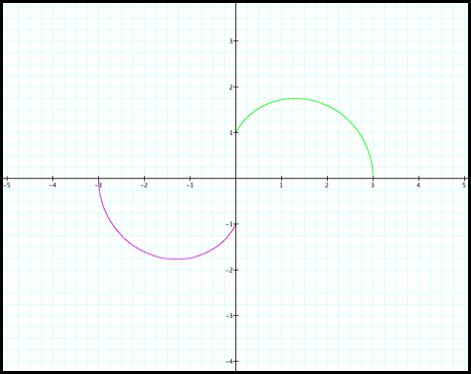
Fig 8d.

5) r increases from -1 to 0, as q increases from 3pi/2 to 5pi/3 (fig8e).

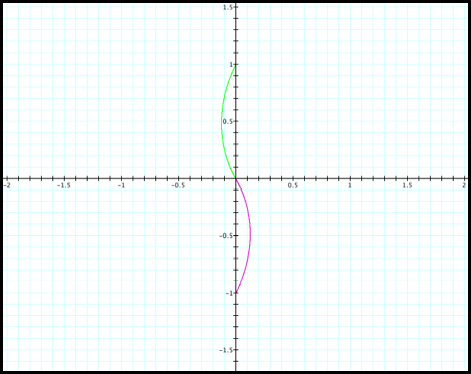
Fig 8e.

6) r increases from 0 to 1, as q increases from 5pi/3 to 2pi (fig8f). Now we are back to positive r values.

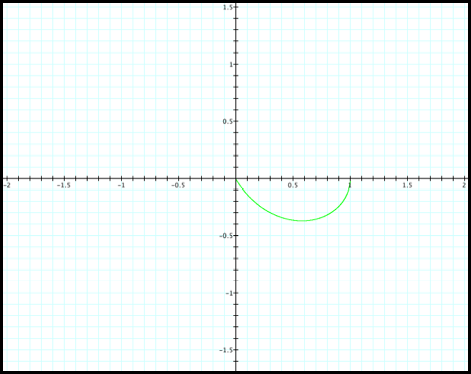
Fig 8f.

We notice similar results for various values of a and b such that a is less than b (fig9).

Case 9: r = 1+2cosq, r = -1+3cosq, and r = -2+4cosq

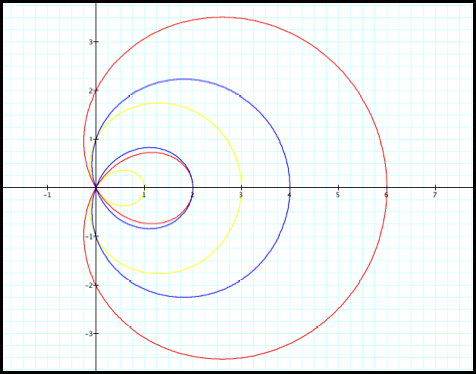
Fig9.

Case 10: r = 7 +6cosq and r=6+7cosq.

The two graphs in Case 10 are very similar. In one equation the b value is greater than a. So in the purple graph the “loop” is missing.

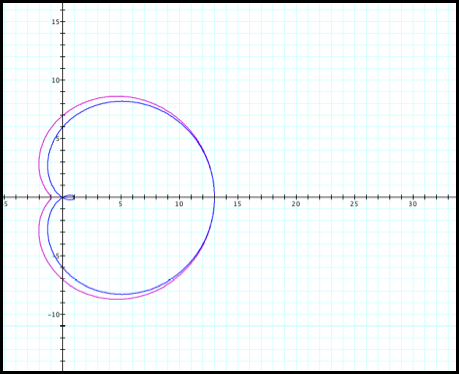
Fig10.

Lets compare the rectangular coordinate graphs in Case 10.

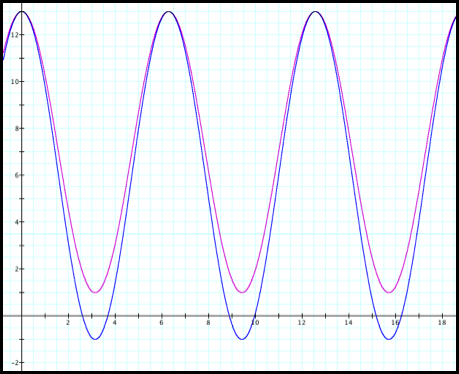
In both instances r begins at 7. Notice that in the blue graph the r value reaches zero and then goes to -1. Thus when b is bigger than a, or when its stretch is bigger than the vertical shift, the graph takes on an “extra” r value which accounts for the “loop.”

Now what if there was no vertical shift?

Consider Case 11: r = 2cosq (fig11).

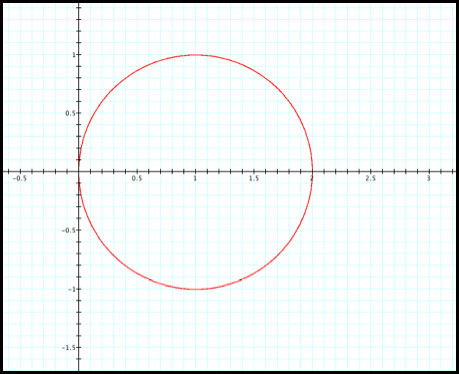
fig 11.

Case 11 appears to be a circle with radius of 2. Lets look at the rectangular coordinate for this case:

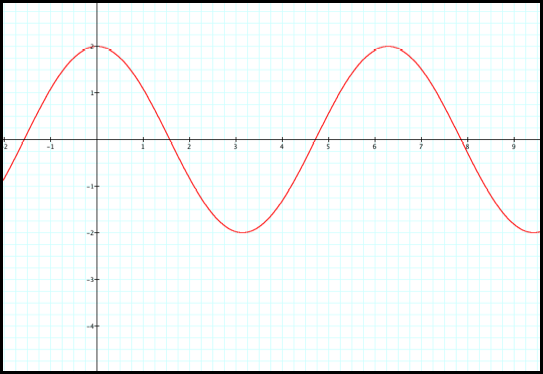
We will run into the negative r values again. Lets look at the progression in polar coordinates:

1) r decreases from 2 to 0 as q increases from 0 to pi/2

2) r decreases from 0 to -2 as q increases from pi/2 to pi.

It appears that we complete the full circle in the interval from 0 to pi. Again the number in front the cosine appears to determine the radius of the circle. Lets look at other illustrations (fig12).

Case 12: r = 4cosq, r = 3cosq, and r = .5cosq

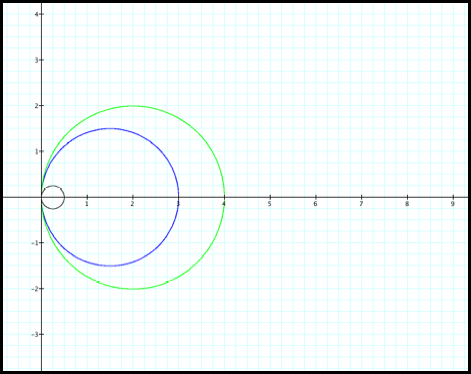
Fig 12.

Next, we’ll look at equations with no vertical shift but with different periods.

Case 13: r = cos(3q). How do you think this graph will look? Remember the period is changed. As you may have expected we get similar results as with Cases 2 through 7 without the effect of the vertical shift (fig 13).

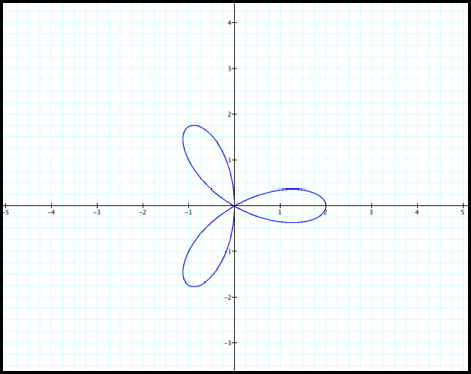
Fig 13.

Comparing Case 11 with an equation with a vertical shift such as r = 1+cos3q (fig13b) you see how the vertical shift affects the graph.

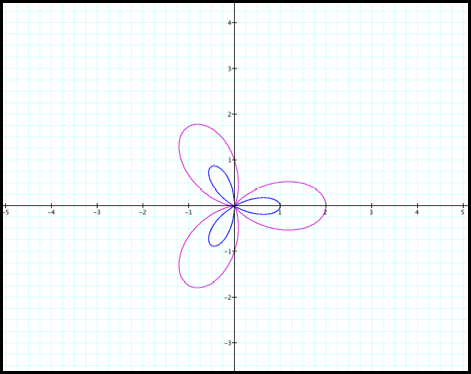
Fig 13b

We investigated both rectangular and polar coordinate graphs of r = a + bcos(kq). We started with cases where a and b are the same

with various k values. Then, we looked at cases where a and b were different but with k value of 1. Lastly, we looked at equations

where a is zero with various b and k values.

You will now work in groups to explore and explain:

1) The cases where a and b are different with various k values.

2) The cases involving the equation r = a + bsin(kq).

RETURN