The Best Angle to Kick a Field Goal from the Hash

By Paulo Tan

I’ve watched many NCAA football games over the years. Kicking field goals in college football seems tough from the hashes, specially the closer the to the goal line. Commentators often say that the kicker has a tough kicking “angle.” Some coaches may even consider taking a penalty, moving the spot of the ball farther from the goal line, to give the kicker a better kicking “angle.” Visually this argument seems logical. Are these commentators and coaches correct? They have convinced me. I decided to investigate this argument mathematically.

I used Geometer’s Sketchpad to model the kicking angle of a field goal. In college football the uprights are 18.5 feet wide. In figure 1, line segment BC represents the width of the field goal. Line AD represents the hash mark, which is 10.75 feet from each upright. The kicker kicks from point A. Remember the hash mark line, AD, is perpendicular to the field goal line, BC. Hence, angle BAC represents the kicking angle.

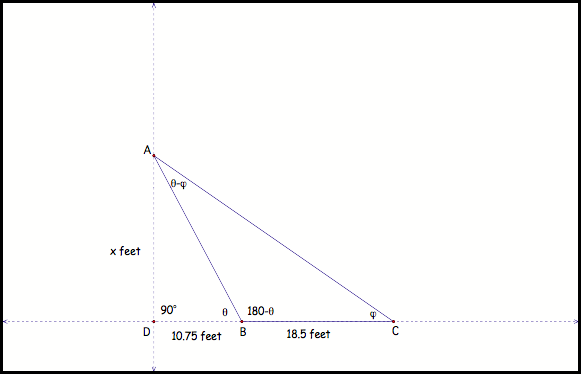
fig1.

Next, I used Sketchpad’s capabilities to analyze the different kicking angles as the kicking distance (point A) is moved closer along the hash mark. Click HERE for an interactive model of the different kicking angles. It seems like the kicking angle increases starting from point D and moving away from line BC along line AD. At some point (lets call this the optimum kicking point) on line AD the kicking angle stops increasing and starts to decrease as point A moves away from this point.

The kicking angle seems like it could be modeled by a function. Thus, using the scale representation in fig1, I applied some basic trigonometric properties to derive the kicking angle as a function of distance.

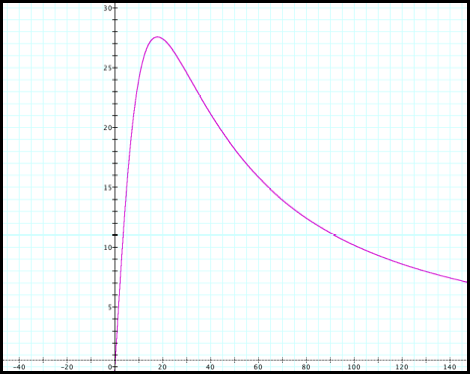
Thus f(x) represents the kicking angle in degrees and x represents the perpendicular distance, in feet, on the hash mark away from the back of the end zone.

Next, I used calculus to pinpoint the exact distance that will give the kicker the best angle.

Since the slope is zero at the maximum point of the function,

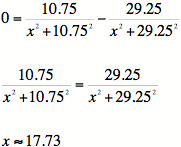
Hence the optimum kicking point is 17.73 feet or 5.91 yards. The kicking angle from 17.73 feet is 27.55 degrees. The optimum kicking point would be from the end zone since the end zone is already 10 yards. The minimum kicking distance in a college football game would be if the be ball is downed near the goal line. The football would then be hiked and placed 7 yards from the goal line which would be at 17 yards from the back of the end zone. The kicking angle at this distance would be 17.93 degrees. From there, the kicking angle decreases according to f(x) as the kicker moves further back.

Suppose a kicker is to attempt a 25-yard field goal from the hash mark. The coach believes moving the kicker back five yards will give the kicker a better angle. According to the function, a 25-yard field goal attempt gives the kicker a 13-degree kicking angle. On the other hand, moving back five yards decreases the kicking angle to 11.2 degrees. Therefore, in trying to give the kicker the best shot at making the field goal, the coach is actually diminishing the kickers chance by decreasing the kicking angle and increasing the kicking distance.

Psychology, field and whether conditions, and many other factors contribute to a kicker’s attempt at a field goal. In the end, math is the only undeniable factor.

RETURN