Assignment
3
Investigation
1
Consider
the equation ax2+bx+c and to overlay several graphs of y=ax2+bx+c
for different values of a, b, or c as the other two are held constant.
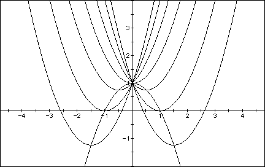
Answer:
We
shall hold 2 of the variables constant and allow a, b, or c to equal -3, -2,
-1, 0, 1, 2, or 3.
First,
letÕs explore a and leave b and c constant:
Equations:
á
y
= -3x2 + bx + c
á
y
= -2x2 + bx + c
á
y
= -1x2 + bx + c
á
y
= 0x2 + bx + c
á
y
= 1x2 + bx + c
á
y
= 2x2 + bx + c
á
y
= 3x2 + bx + c
Graph:
Clearly,
the negative variables for a open downward while the positive variables for a
open upward, all of the graphs pass through the point (0,1), and they all have
different vertices
Next,
letÕs explore b and leave a and c constant:
Equations:
á
y
= x2 - 3x + c
á
y
= x2 - 2x + c
á
y
= x2 - 1x + c
á
y
= x2 - 0x + c
á
y
= x2 + x + c
á
y
= x2 + 2x + c
á
y
= x2 + 3x + c
Graph:
As
before, all of the graphs pass through the point (0,1) on the y-axis, open
upward, and have different vertices.
Finally,
letÕs explore c and leave a and b constant:
Equations:
á
y
= x2 + bx - 3
á
y
= x2 + bx - 2
á
y
= x2 + bx - 1
á
y
= x2 + bx + 0
á
y
= x2 + bx + 1
á
y
= x2 + bx + 2
á
y
= x2 + bx + 3
Graph:
Once
again all of the graphs open upwards and have different vertices. None of the
graphs share the same coordinate points, and as c increases the vertices of the
graphs shift up as well.