Assignment
8
Investigation
11
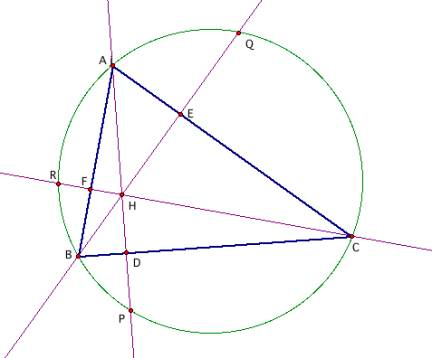
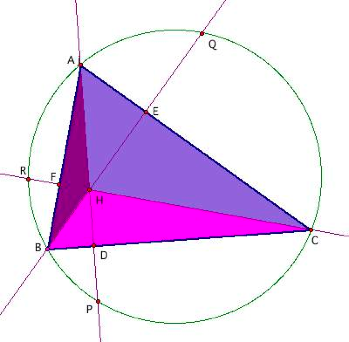
Construct
any acute triangle ABC and its circumcircle. Construct the three
altitudes AD, BE, and CF. Extend each altitude to its intersection with
the circumcircle at corresponding points P, Q, and R.
Answer:
Claim:
![]()
Proof
of Claim:
First
break the segments into ratios as follows:

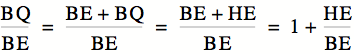

Next
we add:
![]()
to
get:
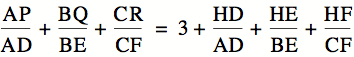
First,
consider the first ratio,
![]()
HD
is the altitude of the triangle BHC and AD is the altitude of the triangle ABC,
so we can use them in the formula for the areas of the triangles BHC and ABC:
So,
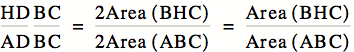
Similarly


So,
plugging in our original equation gives us:
![]()
Note
:
![]()
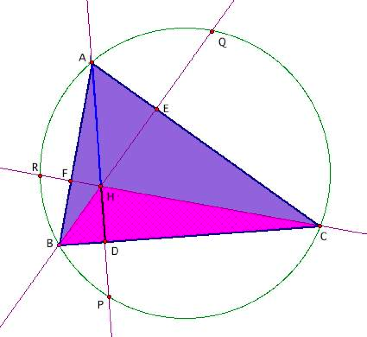
Since,
those three triangles make up the triangle ABC:
And
since
![]() ,
,
We
get that
![]() .
.