Assignment
9
Investigation
2
Let
triangle ABC be any triangle. Then if P is any point in the plane, then the
triangle formed by constructing perpendiculars to the sides of ABC (extended if
necessary) locate three points R, S, and T that are the intersections. Triangle
RST is the Pedal Triangle for Pedal Point P.
What
if pedal point P is the centroid of triangle ABC?
Answer:
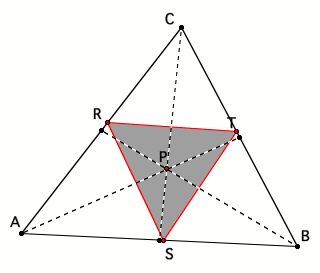
First,
letŐs look at a construction of a pedal triangle:
The
centroid of a triangle is the point of intersection of its medians (the lines
joining each vertex with the midpoint of the opposite side). The centroid
divides each of the medians in the ratio 2:1. The centroid is also located 1/3
of the perpendicular distance between each side and the opposing point.
LetŐs
use triangle ABC to make pedal point P become the centroid.
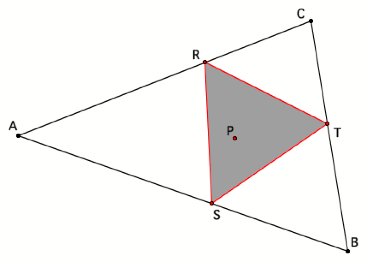
First
we must find the midpoints.
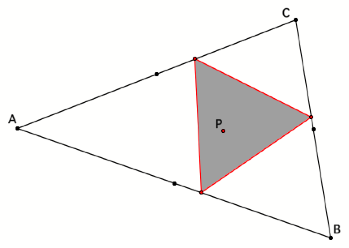
Next,
connect each vertex to its opposites sidesŐ midpoint.
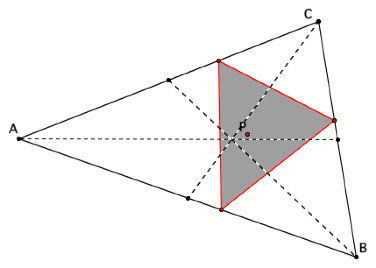
Finally,
drag pedal point P to the intersection of the three segments that are
connecting vertices and midpoints.