Exploring Parametric Equations

By

Princess Browne

Investigation. Consider the parametric equations

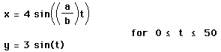
Graph these for

Describe fully. You may have to increase the range of t for the larger fractions. This class of parametric curves is called the Lissajous curves. Compare with

x = sin ((a) t)

y = sin ((b) t)

I will start by graphing the parametric equation of x = sin ((a) t) and y = sin ((b) t). Next, I will graph the parametric equations of x = 4 sin((a/b)t) and y = 3 sin(t). Finally, I will compare the different Lissajous curves.

When a=4, b=1

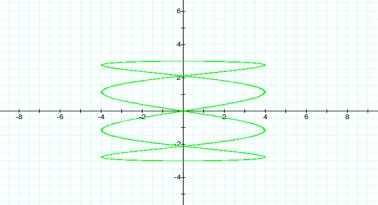
When a=5, b=1

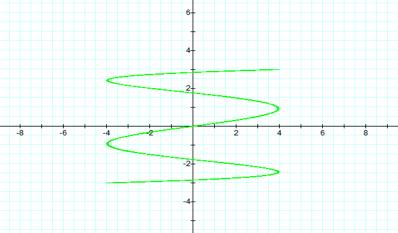
When a=1, b=4

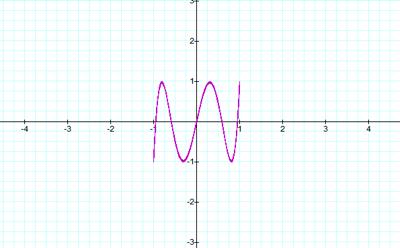
When a=1, b=5

From the graphs above, we will notice that when a > b the frequency of the curve is oriented around the y-axis, and when a < b the frequency of the curve is oriented around the x-axis. When a and b have common even or odd factors we cannot classify any curves because the graph forms a straight line. The curve formed is determine from the value of a/b. The amount of times the curve crosses the x-axis and the y-axis are determine by the value of a/b. For instance, if a/b is 1/2, the graphs will form a close curve along the x-axis. If a/b is 1/3 the graph will form an open curve along the x-axis.

Next, we will look at the following parametric equation:

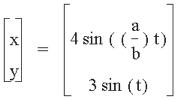
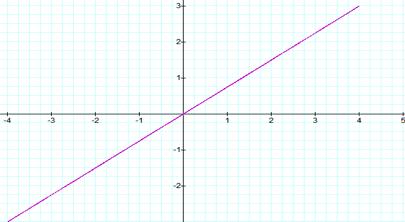
When a=b=1

When a=b we have a straight line

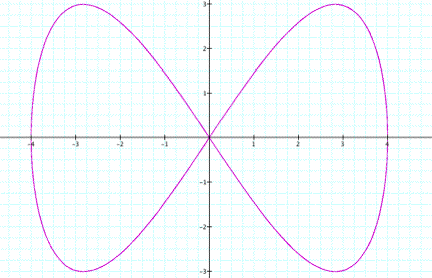
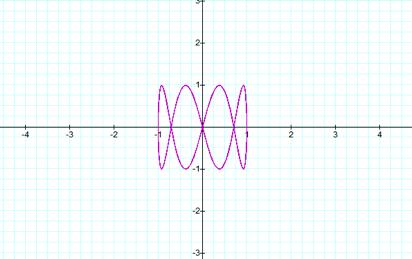
When a=1, b=2

When a=1 and b=2 we have a bowtie

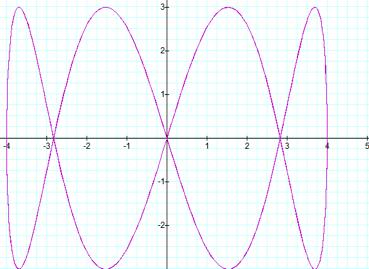
When a=1, b=4

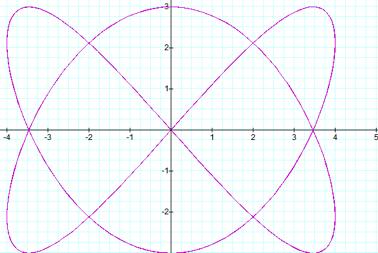
When a=2, b=3

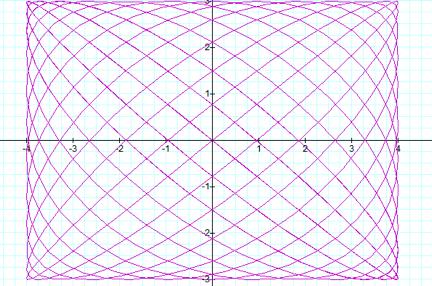
When a=12, b=13 (t-50 to 50)

From the following graphs, we can conclude that the graph of parametric equations is dependent on the values of a/b. The periods of the graphs are the same why the frequency for each graph changes because the frequency depends upon the values of a/b.

Using the parametric equations x = 4 sin ((a/b) t) and y = 3 sin (t)

x = sin ((a)t) y = sin ((b)t)

When we compare the graphs from the two equations; we will notice that there is a difference between the graphs. The graphs of x = 4 sin((a/b)t) and y = 3 sin(t) all have the same dimensions of (4,0), (-4,0), (0,3), and (0,-3). Whereas the graphs for x = sin ((a) t) and y = sin ((b) t) dimensions depends on the value of a. For instance when a< b we have the dimensions of (1,0), (-1,0), (0,1), and (0,-1) and when a > b the dimensions ions are (4,0), (-4,0), (0,3), and (0,-3).

Return