Exploring Polar Equations

By Princess Browne

Investigate

Note:

- When a and b are equal, and k is an integer, this is one textbook version of the “n-leaf rose."

- Compare with

For various k. What if . . . cos ( ) is replaced with sin ( )?

r = b sin (kq)

We will start this investigation by graphing the function of

r = a + b cos (kq)

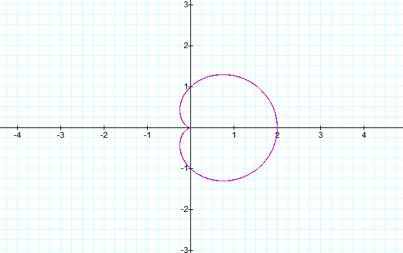
a=b=k=1

The following function gives us a cardiod, which is known as the textbook version of the ‘n-leaf rose’. We want to graph the function leaving k as a constant and change the values of a and b. Next, we will graph the function leaving a and b constant and change the values of k. Finally, we will compare the equations by using the different graphs.

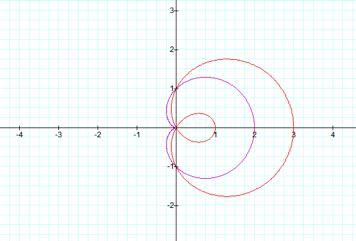
Purple r = a + b cos (kq), Red r = a + 2 cos (kq)

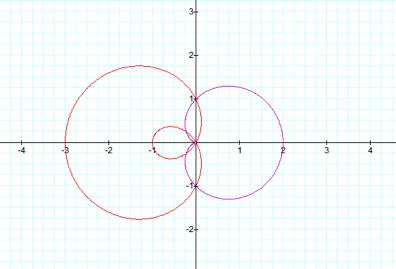
Purple: r = a + b cos (kq), Red: r = a - 2 cos (kq)

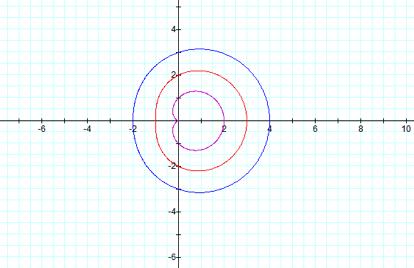
Purple: a = 1, Red: a = 2, Blue: a = 3

When a and b are constant and k varies

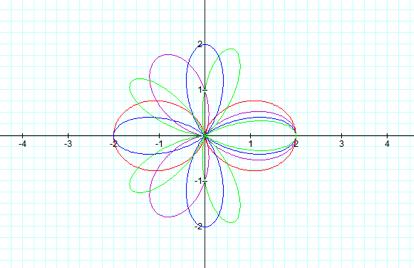
Red: k = 2, Purple: k = 3, Blue: k = 4, and Green: K = 5

Next, we will look at r = b cos (kq)

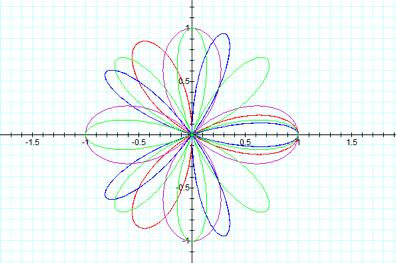
Purple: K = 2, Red: K = 3, Blue: k = 5, Green: k =4

Basally, k indicates the number of leaf rose the graph creates. When k is an odd integer the graph will create a rose with k petals. When k is an even integer, the graph will create a rose with 2k petals. For instance, if k = 3 the rose will produce a rose with 3 pedals and if k = 4 the rose will produce a rose with 8 pedals.

Finally, we will graph the equations using sine instead of Cosine!

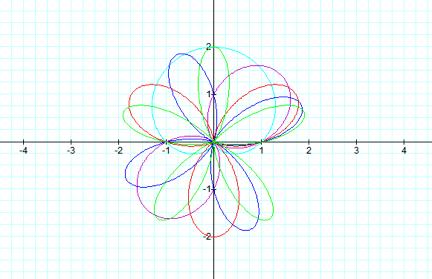
Teal: r = a + b sin (kq)

Purple: r = a + b sin (2q)

Red: r = a + b sin (3q)

Blue: r = a + b sin (4q)

Green: r = a + b sin (5q)

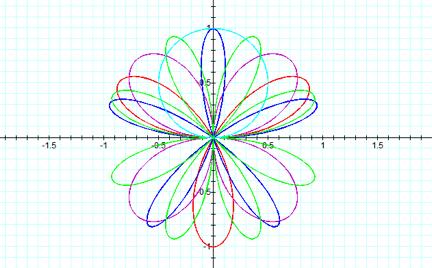
Teal: r = b sin (kq)

Purple: r = b sin (2q)

Red: r = b sin (3q)

Green: r = b sin (4q)

Blue: r = b sin (5q)

The graphs rotate towards the y-axis. The value of k also determines the number of pedals created. We can see that the graphs with sine and cosine are the same with the exception of the rotation.

Return