Triangle medians

By

Princess Browne

We will construct a triangle and its medians. Then, we will construct a second triangle with the three sides having the lengths of the three medians from the first triangle. Finally, we will find the relationships between the two triangles. Some examples of the relationship are as followed: are they congruent? Similar? have same area? same perimeter? ratio of areas? ratio or perimeters?

I will start by constructing triangle number 1 and its medians. Then, I will construct triangle number 2 using the medians of triangle number 1.

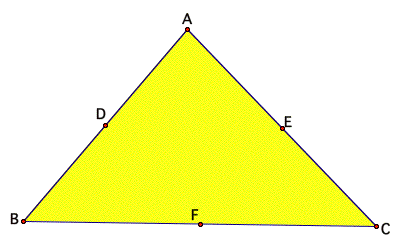
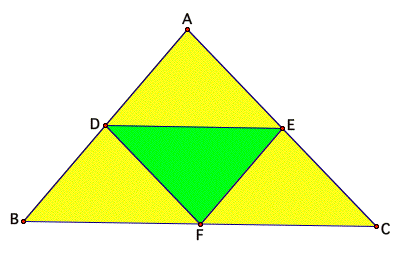
Given DABC, let the points D, E, and F be the midpoints of segments AB, AC and BC. I know that segment AD » DB, AE »EC, and BF » FC by the definition of midpoints. If we connect the three midpoints to form triangle number 2, we will end up with a median triangle.{ERROR. The medians are segments from a vertex to the midpoint of an opposite side.} By the definition of a mid segment of a triangle I know that the mid segment of DABC is DE. I also know that segment DE is 1/2BC, DF is 1/2AC, and EF is 1/2AB. With this information I know that DABC and DDEF have a ratio that is 2:1. A ratio of the perimeters that is 2:1.

Below are the lengths of the different segments

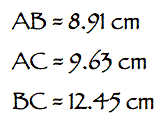
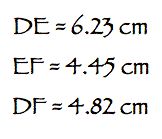
However, the ratio of the area of these triangles is different from the ratio of the perimeter because there are four of the smaller triangles within the original triangle. Therefore we can conclude that the ratio of the area of a triangle to it’s median is 4:1.

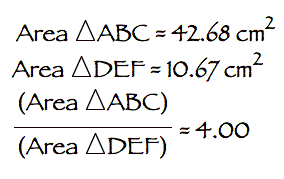
since the ratios of the sides are not always the same the triangle are not similar, but the perimeters and areas of the two triangle will always have the same ratio. The relationship between the two triangles is when the original triangle is an isosceles triangle the median triangle will also be an isosceles triangle. This is also true for right triangles, obtuse triangles and equilateral triangles

Return