
Exploring Tangent Circles
By Princess Browne
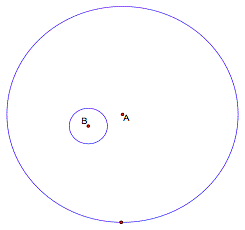
Given two circles A and B we need to construct a third circle C
that is tangent to both circle A and circle B. We know that when two circles
are tangent they share a common point. Therefore we will start this
investigation by creating circle A and circle B.
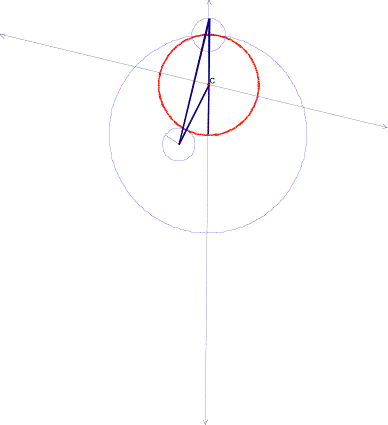
To construct a circle tangent to Circle A and circle B we will construct
a point on circle A or a point on circle B. Then we will construct the radius
of circle B and a line through the center of circle A. Next, we will construct a
circle CÕ from the radius of circle B. We will create a segment from the center
of circle B to the point on circle CÕ. Then we will construct a triangle from
the two points on the line and the point from circle A. Next, we will find the
midpoint of the segment and create a perpendicular line to help with the
construction of circle C. We will find the point, where the perpendicular
bisector intersects the line that passes through circle B which is the center
of circle C.
Next we will look at the loci of tangent
circles
The picture below
indicates that when the two circles intersect the trace of the loci form is
still an ellipse that shows the circles intersection points.

The next picture
will show that when circle A and Circle B does not intersect the trace of their
loci forms a hyperbola

For further illustrations, lick the GSP
Files below