Experiments with Linear Functions

Karyn Carson

Now that we’ve covered linear functions, let’s examine what we can do with them.

Take two linear functions, f(x) and g(x) and graph them.

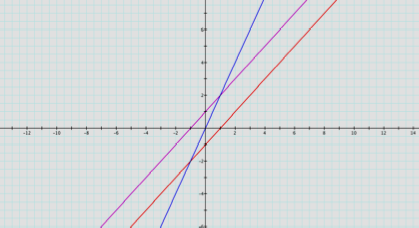
For example: f(x) = (x+1) and g(x) = (x-1).

If you add the two expressions, you get a new function, h(x) = 2x. What kind of graph is this?

What happens if you multiply the expressions, f(x) and g(x)? What will the graph look like?

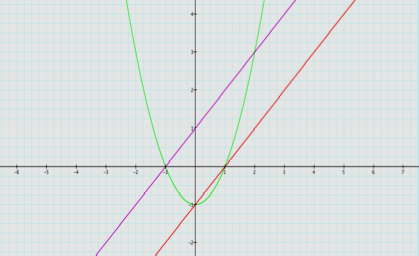
Again, graph the linear functions of f(x) = x+1 and g(x) = x-1 and then graph their product.

The product of the expressions is h(x) = x² – 1. How is this graph different from the original graphs? How is the function different from the original functions?

This graph is called a parabola. The equation is different because the x is raised to the second power.

What do you think will happen if we divide the original linear functions? Let’s see…

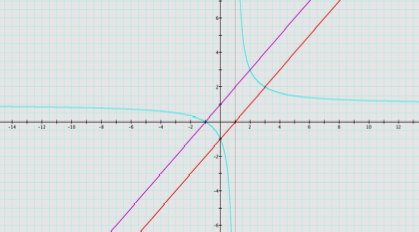
If you divide the two linear expressions (this is as simple as it gets):

x+1

x -1

you notice something new. What happened to the graph? Do you know what shape it has now become?

This is called a hyperbola.

Now, let’s see what happens if our ‘x’ in the f(x) function is set equal to our g(x) function (this is called a composite function):

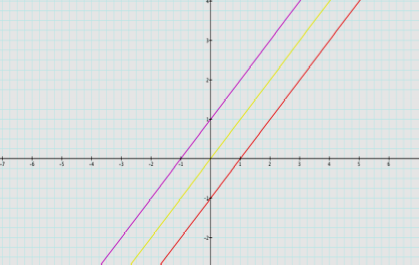
[(x-1) +1] = h(x)

x = h(x)

What would this graph look like?

This, again, is a linear function. What is it’s relationship to f(x) and g(x)?

It is parallel.

Let’s continue our investigation. Do all of these observations only occur with the functions I have explored with you? I’d like for you to investigate these same relationships with your own linear functions. Make up two linear functions and perform all the operations we performed today (add, multiply, divide and combine). When we come back together, let’s discuss your findings.

Example #2:

f(x) = 2x + 3 and g(x) = x – 8

SUM: (2x + 3) + (x – 8)

3x – 5

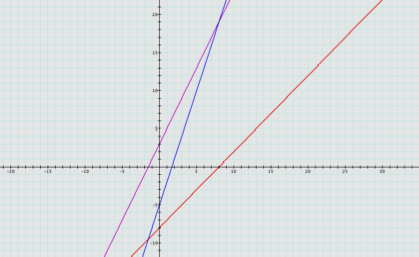
h(x) = 3x – 5 line

PRODUCT: (2x + 3) (x – 8)

2x² – 13x – 24

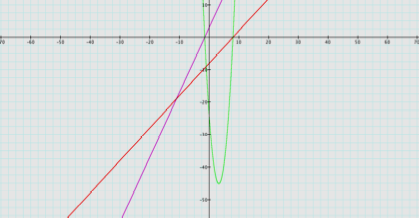
h(x) = 2x² – 13x – 24 Parabola

QUOTIENT: 2x + 3/x-8

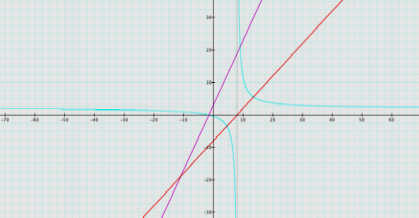
h(x) = 2x + 3

x – 8 Hyperbola

COMPOSITE: 2(x – 8) + 3

2x – 13

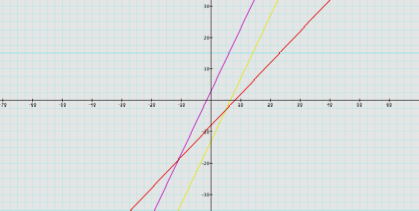
h(x) = 2x – 13 line, parallel to f(x)

Will all quotients of linear functions result in a hyperbola?

What if the denominator is a factor of the numerator?

Use f(x) = 6x – 3 and g(x) = 2x – 1.

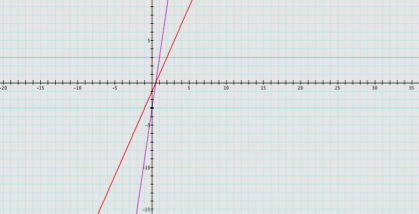
6x - 3

2x – 1 = 3/1, so y = 3.

Will all composite functions be parallel to f(x)?

No:

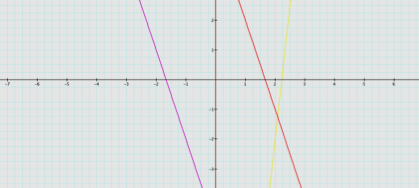
If f(x) = -3x + 5 and g(x) = -3x – 5, then f(g(x)) will have a positive slope, as opposed to the original functions. Regardless, the composite function will be linear.

In conclusion:

The sum of linear expressions will result in a line, because the degree of the resulting function is one.

The product of linear expressions will result in a parabola, because the degree of the resulting function is two.

Based on my examples, the quotient of linear expressions will result in a hyperbola, unless the denominator is a factor of the numerator. The reason the hyperbolas result from some of the quotients is because the value of x has limitations in that the denominator cannot equal zero.

Composite functions will result in a line, but not necessarily parallel to the original function. It’s a line because the degree of the function will always be one.

Back to Karyn’s Homepage