Altitudes and Orthic Triangles

Karyn Carson

Construct triangle ABC and its circumcircle:

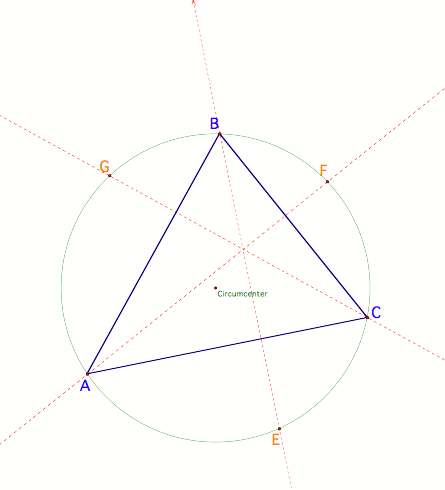
Next, construct the altitudes of triangle ABC and mark their intersections on the circumcircle:

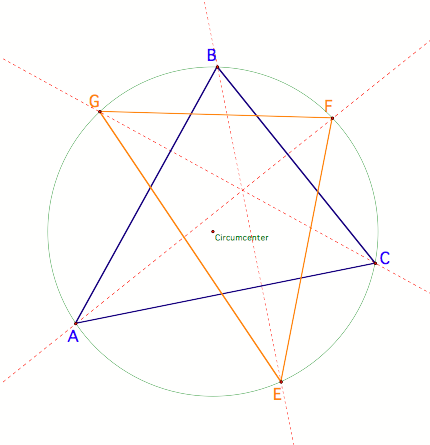
Then, construct the triangle that is formed from those intersections:

If you construct the orthic triangle (HIJ), you will see that it and the triangle formed by the altitudes (EFG) of the original triangle (ABC) are similar. At least it looks that way. Let’s investigate using information on parallel lines.

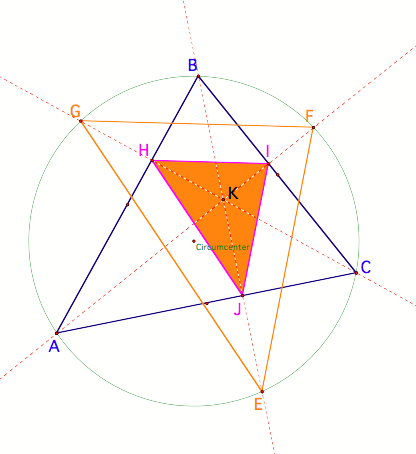
If I can prove that HI is parallel to GF, and IJ is parallel to FE, and JH is parallel to EG, then the triangles must be similar. To start with, segment AB is a transversal of segments HI and GF. Then we need to look at the angles formed by that transversal, BHI and GmH (alternate interior angles).

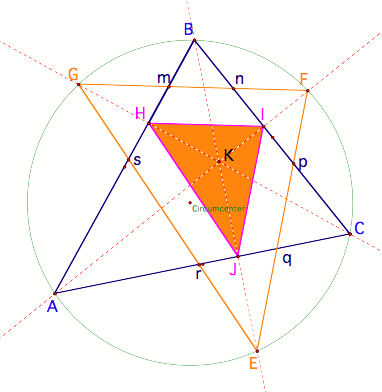
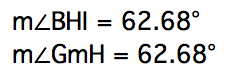
If a transversal crosses two lines or segments that are parallel, then their alternate interior angles must be equal. In this case they are, so the segments must be parallel.

We can also measure the angles for the other segments to prove that they are parallel:

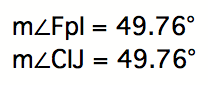
and

What happens if it’s a different triangle. Will this proof still work?

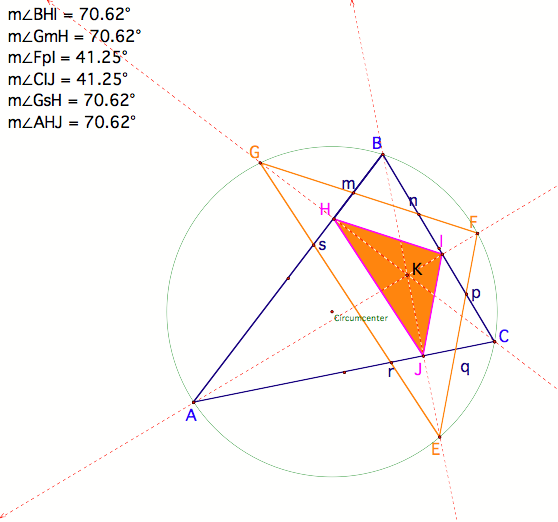
The alternate interior angles are still congruent, so therefore the triangles are still similar.

What happens if we make our original triangle obtuse? What happens to our similar triangles?

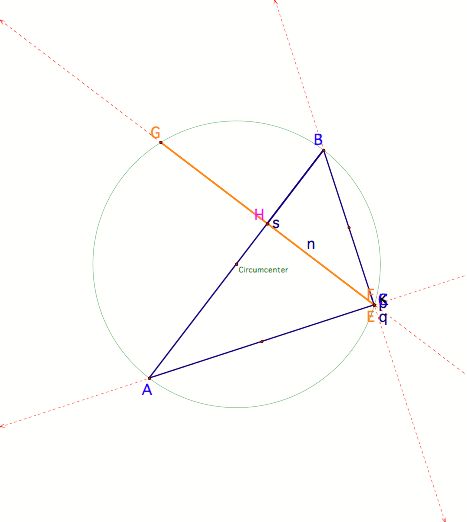
When angle C becomes a right angle, the orthocenter becomes the same point as C and we lose our orthic triangle as well as the ‘altitude’ triangle. If angle C becomes obtuse,

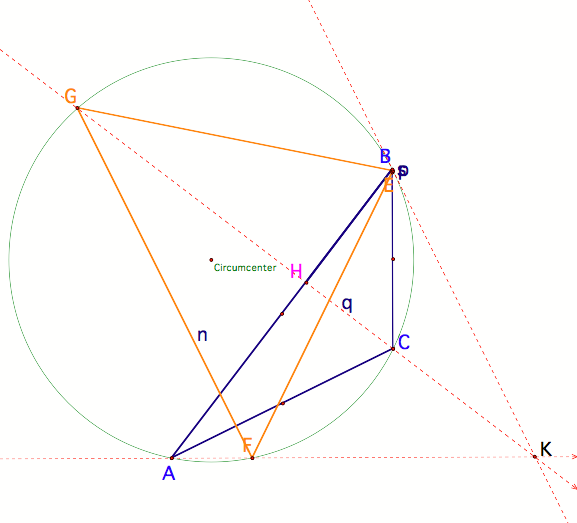
then the orthocenter leaves triangle ABC, because two of the altitudes have also left the triangle (they must be drawn outside the triangle to be perpendicular with the base).

Back to Karyn’s Homepage