
Land Surveying
Karyn Carson
According
to Wikipedia, land surveying is Ōthe technique and science
of accurately determining the terrestrial or three-dimensional space position of points and the distances and
angles between them.Ķ There are several types of surveys: boundary,
topographical, as-built, construction, and geological are just a few. Mathematics is used throughout
surveying and is instrumental in determining the position of objects. Also, mathematics is used in the business
side of surveying. Many people who
are surveyors have their own business and must know how their company is
run. How much do they spend on
labor, benefits, facilities? How
much should they charge for a survey?
IÕve looked at Principles and Practice of Land
Surveying: Sample Examination
by George M. Cole (Professional Publication, Inc., 2003) and collected several
problems to show some of the ways mathematics is used in surveying.
1. Land
Description
Lot 1, Block A of Silver Lake
Plantation Subdivision as recorded in Plat Book 1 of the public records of
Jefferson County, Florida;
Less and Except the western
1/4 of said Lot 1; and
Less and Except a portion of
said Lot 1 described as follows:
Begin at the intersection of the south line of said Lot 1 and the west
line of Section 12, Township 2 North, Range 5 East; then go northerly along
said section line for 250 ft; then go easterly in a straight line for 660 ft
more or less to the east line of said Lot 1; then go southerly for 250 ft along
said east line to the southeast corner of said Lot 1; then go westerly along
the south line of said Lot 1 for 500 ft more or less to the Point of Beginning;
containing 3.79 ac more or less.
Lot 1 Dimensions per Survey
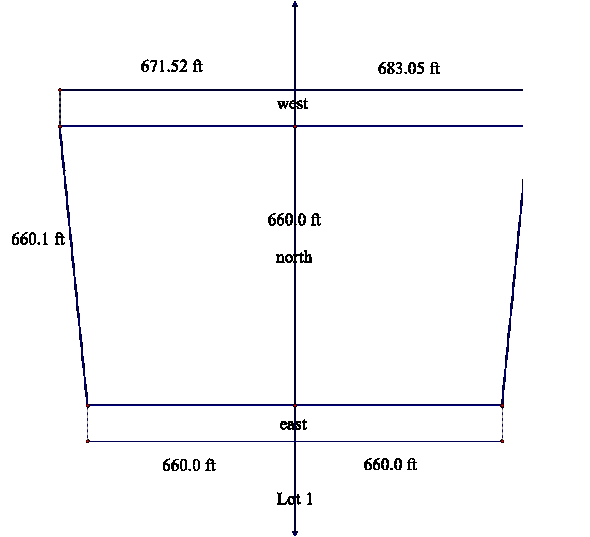
a. What is
the total acreage of Lot 1 based on the survey data?
b. What
is the acreage of the land excepted from Lot 1 by the first Less and Except
parcel?
![]()
Solutions:
a. To
solve this problem, we would first have to separate the piece of land into
three shapes: a rectangle and two
right triangles.
1320 ft
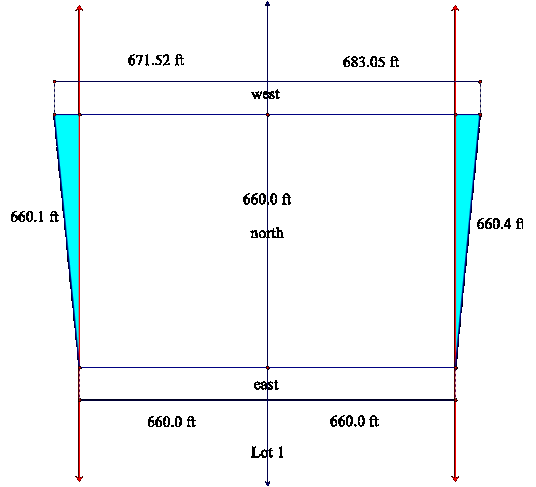
By creating perpendicular segments to the northern side
of the property, we create three
segments which now become the bases of our rectangle and two right triangles.
The base of the rectangle is 1320 feet (660.0 + 660.0)
and the height is 660 feet; therefore the area of the rectangle is 871200 sq.
ft. Now, letÕs look at the
triangles.
We must find the measurements of the bases of the two
triangles. How can this be
determined?
To find the base of the western triangle, simply subtract
660 ft from 671.52:
671.52-660 = 11.52 ft
To find the base of the eastern triangle, subtract 660
from 683.05:
683.05-660 = 23.05 ft
Remember, to find the area of a triangle, you take half the
product of the base and the height.
Area of western triangle:
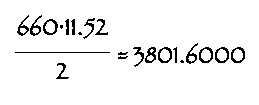
Area of eastern triangle:
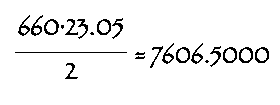
And now to find the total area:
Atotal = 871200 + 3801.6 + 7606.5
Atotal = 882608.1 sq. ft
Because there are 43560 sq. ft in an acre, we must divide
the total area by this number to calculate the number of acres in our property:
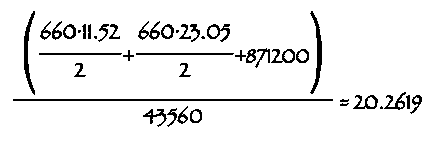
b. To
find the Less and Except portion of the lot, just find ¼ of the total
acreage:
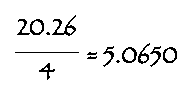
Another problem from the
Sample Examination:
2.
Land
Description
All land in Section 7 lying
northerly and easterly of State Road 99:
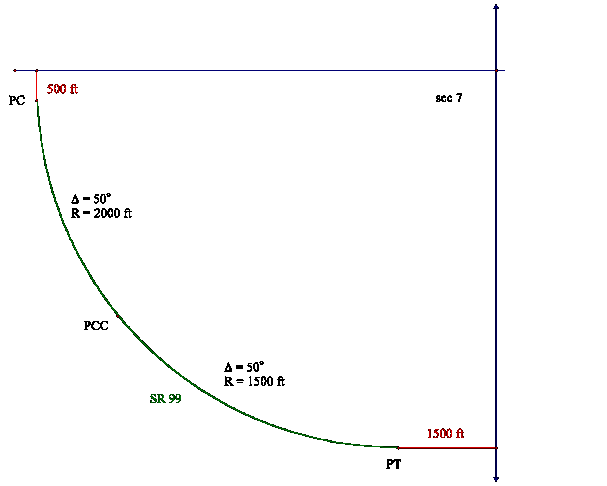
What is most nearly the
distance along the centerline of State Road 99 within section 7?
Solution:
For curve 1, find the arc length, L, by taking the
measure of the interior angle, dividing it by 360 degrees and multiplying by
2(pi)r:
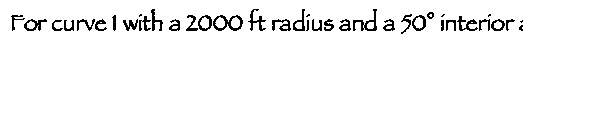
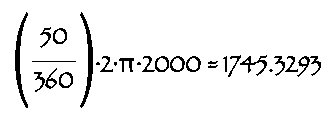
For curve 2, do the same:
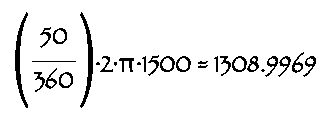
The total distance, Dtotal, is:
Dtotal = tangent1 + L1 +
L2 + tangent2
=
500 ft + 1745.33 ft + 1309.00 ft + 1500 ft
=
5054.33 ft
Also, from a business sense, there are many instances
where knowledge of mathematics will come in handy.
Results from an audit for a firm are as follows:
|
Item |
Cost ($) |
|
Direct labor |
3,682,957 |
|
Allowable fringe benefits |
1,577,283 |
|
Allowable general overhead |
4,684,247 |
|
Facility cost of capital |
90,621 |
1.
What is most nearly the factor for
combined fringe benefits and general overhead for the firm on a direct labor
basis?
The total overhead factor is the ratio of the sum of fringe
benefit costs and general overhead costs to direct labor costs:
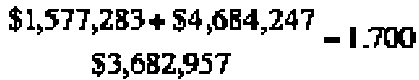
This is equal to 170%.
2. For a
project involving $250,000 in direct labor costs, what would most nearly be the
total cost to the firm of producing the services for the project neglecting
facility cost of capital?
To find the project cost, you must first find the product
of the direct labor cost and the overhead rate, then add that to the direct
labor cost:
![]()
3. Assuming
that a 15% operating margin on total cost is desired, approximately what fee
should be charged by the firm for the project described in the previous
problem, neglecting facility cost of capital?
Well, 15% of $675,000 is $101,250 – now add that
amount to the project cost:
$675,000 + $101,250 = $776,250
4. What
is most nearly the facility capital cost of money (FCCM) rate for the firm, on
a direct labor basis?
We need to compare the facility cost to the direct labor:
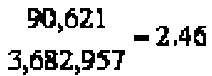
Approximately 2.5% of the direct labor for the project should
be charged for the facility cost.
5. How
much should this be for the project outlined in the previous problems?
2.5% of $250,000 is $6,250.
6. What
is the total bid for this project?
$675,000 + $101,250 + $6150 = $782,400