|
Michelle E. Chung |
*
EMAT6680 Assignment 12: Fibonnaci Sequence |
|
4. Generate a Fibonnaci Sequence in the first column using F(0)=1, F(1)=1,
f(n) = f(n-1) + f(n-2).
a. Construct the ratio of each pair of adjacent terms in the Fibonnaci sequence.
What happens as n increases?
What about the ratio of eery second term? etc.
b. Explore sequences where f(0) and f(1) are some arbitary integers other than 1.
If f(0)=1 and f(1)=3, then your sequence is a Lucas Sequence.
All such sequences, however, have the same limit of the ratio of successive terms.
|
 |
a. Fibonnaci Sequence
| Fibonnaci Sequence Table
w/its ratios
|
|
|
n |
Fibonnaci Sequence |
f(n)/f(n-1) |
f(n)/f(n-2) |
f(n)/f(n-3) |
f(n)/f(n-4) |
1 |
1 |
|
|
|
|
2 |
1 |
1 |
|
|
|
3 |
2 |
2 |
2 |
|
|
4 |
3 |
1.5 |
3 |
3 |
|
5 |
5 |
1.666666667 |
2.5 |
5 |
5 |
6 |
8 |
1.6 |
2.666666667 |
4 |
8 |
7 |
13 |
1.625 |
2.6 |
4.333333333 |
6.5 |
8 |
21 |
1.615384615 |
2.625 |
4.2 |
7 |
9 |
34 |
1.619047619 |
2.615384615 |
4.25 |
6.8 |
10 |
55 |
1.617647059 |
2.619047619 |
4.230769231 |
6.875 |
11 |
89 |
1.618181818 |
2.617647059 |
4.238095238 |
6.846153846 |
12 |
144 |
1.617977528 |
2.618181818 |
4.235294118 |
6.857142857 |
13 |
233 |
1.618055556 |
2.617977528 |
4.236363636 |
6.852941176 |
14 |
377 |
1.618025751 |
2.618055556 |
4.235955056 |
6.854545455 |
15 |
610 |
1.618037135 |
2.618025751 |
4.236111111 |
6.853932584 |
16 |
987 |
1.618032787 |
2.618037135 |
4.236051502 |
6.854166667 |
17 |
1597 |
1.618034448 |
2.618032787 |
4.236074271 |
6.854077253 |
18 |
2584 |
1.618033813 |
2.618034448 |
4.236065574 |
6.854111406 |
19 |
4181 |
1.618034056 |
2.618033813 |
4.236068896 |
6.854098361 |
20 |
6765 |
1.618033963 |
2.618034056 |
4.236067627 |
6.854103343 |
21 |
10946 |
1.618033999 |
2.618033963 |
4.236068111 |
6.85410144 |
22 |
17711 |
1.618033985 |
2.618033999 |
4.236067926 |
6.854102167 |
23 |
28657 |
1.61803399 |
2.618033985 |
4.236067997 |
6.85410189 |
24 |
46368 |
1.618033988 |
2.61803399 |
4.23606797 |
6.854101996 |
25 |
75025 |
1.618033989 |
2.618033988 |
4.23606798 |
6.854101955 |
26 |
121393 |
1.618033989 |
2.618033989 |
4.236067976 |
6.854101971 |
27 |
196418 |
1.618033989 |
2.618033989 |
4.236067978 |
6.854101965 |
28 |
317811 |
1.618033989 |
2.618033989 |
4.236067977 |
6.854101967 |
29 |
514229 |
1.618033989 |
2.618033989 |
4.236067978 |
6.854101966 |
30 |
832040 |
1.618033989 |
2.618033989 |
4.236067977 |
6.854101966 |
31 |
1346269 |
1.618033989 |
2.618033989 |
4.236067978 |
6.854101966 |
32 |
2178309 |
1.618033989 |
2.618033989 |
4.236067977 |
6.854101966 |
33 |
3524578 |
1.618033989 |
2.618033989 |
4.236067978 |
6.854101966 |
34 |
5702887 |
1.618033989 |
2.618033989 |
4.236067977 |
6.854101966 |
35 |
9227465 |
1.618033989 |
2.618033989 |
4.236067977 |
6.854101966 |
| |
|
Golden Ratio |
Square
of
Golden Ratio |
Cubic
of
Golden Ratio |
4th power
of
Golden Ratio
|
|
Scatter Plot
of the Ratios |
|
Ratio1
: f(n)/f(n-1) |
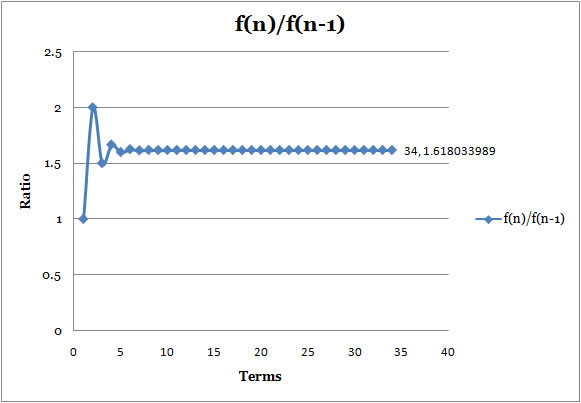
- The first ratio, the ratio of each pair of adjecent terms in the Fibonnaci Sequence, is approaching 1.618033989, which is known as Golden Ratio.
|
Ratio2
: f(n)/f(n-2) |
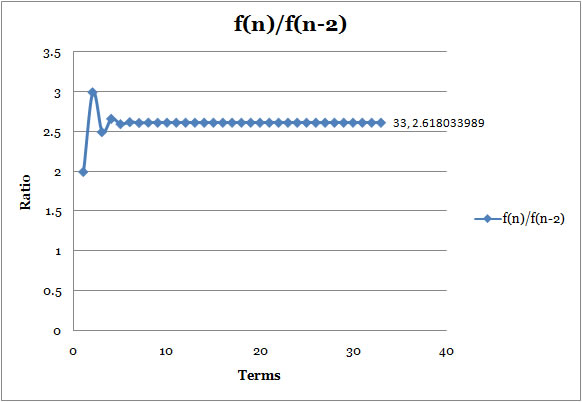
- The second ratio, the ratio of every second term in the Fibonnaci Sequence, is approaching 2.618033989, which is the square of Golden Ratio.
|
Ratio3
: f(n)/f(n-3) |
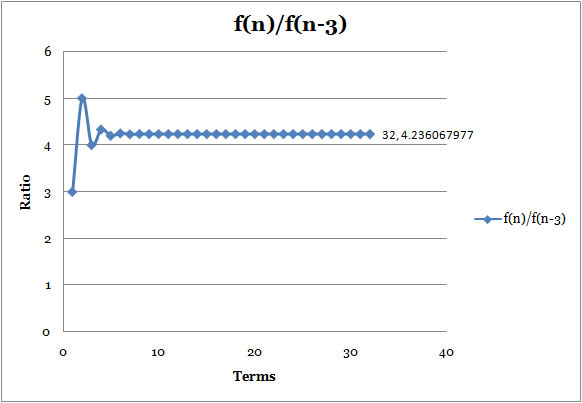
- The third ratio, the ratio of every third term in the Fibonnaci Sequence, is approaching 4.236067977, which is the cubic of Golden Ratio.
|
Ratio4
: f(n)/f(n-4) |
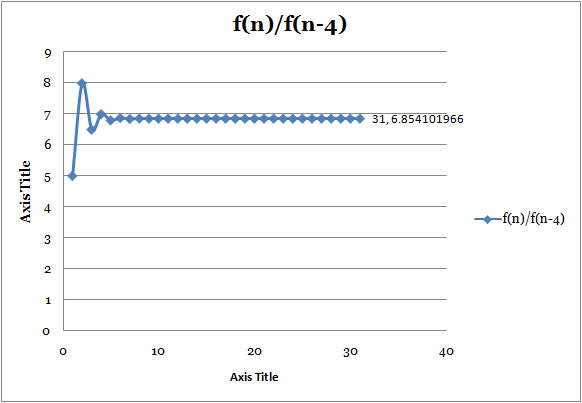
- The forth ratio, the ratio of every forth term in the Fibonnaci Sequence, is approaching 6.854101966, which is the 4th power of Golden Ratio.
|
|
Conclusion |
|
- As n increases, the ratios are bouncing up and down;
however, they are approaching limits of the sequence, which are Golden Ratio, Square of Golden Ratio, Cubic Golden Ratio, 4th power of Golden Ratio, etc. respectively.
So, we can predict, if we calculate f(n)/f(n-5), it would be limited to 5th power of Golden Ratio, and so on.
Let's check it.
Table |
Scatter Plot |
n |
f(n)/f(n-5) |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
8 |
7 |
13 |
8 |
10.5 |
9 |
11.33333333 |
10 |
11 |
11 |
11.125 |
12 |
11.07692308 |
13 |
11.0952381 |
14 |
11.08823529 |
15 |
11.09090909 |
16 |
11.08988764 |
17 |
11.09027778 |
18 |
11.09012876 |
19 |
11.09018568 |
20 |
11.09016393 |
21 |
11.09017224 |
22 |
11.09016907 |
23 |
11.09017028 |
24 |
11.09016982 |
25 |
11.09016999 |
26 |
11.09016993 |
27 |
11.09016995 |
28 |
11.09016994 |
29 |
11.09016994 |
30 |
11.09016994 |
31 |
11.09016994 |
32 |
11.09016994 |
33 |
11.09016994 |
34 |
11.09016994 |
35 |
11.09016994 |
| |
5th power
of Golden Ratio |
|
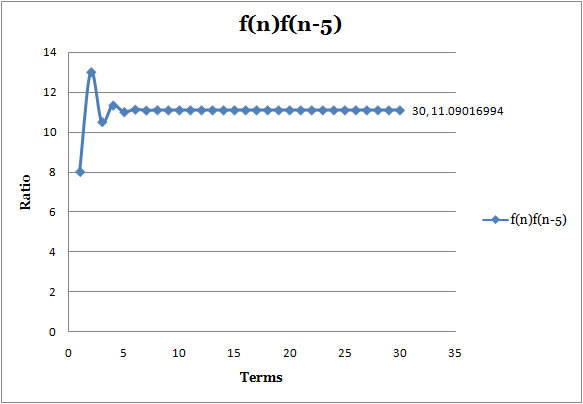 |
From the table, we can assert our conjecture.
- The first terms of the ratios are same as Fibonnaci Sequence.
So, if we take the first term of each ratio and make a sequence, it would be Fibonnaci Sequence.
|
Back to the Top |
b. Lucas Sequence
| Lucas Sequence Table
w/its ratios
|
|
|
n |
Lucas Sequence |
f(n)/f(n-1) |
f(n)/f(n-2) |
f(n)/f(n-3) |
f(n)/f(n-4) |
1 |
1 |
|
|
|
|
2 |
3 |
3 |
|
|
|
3 |
4 |
1.333333333 |
4 |
|
|
4 |
7 |
1.75 |
2.333333333 |
7 |
|
5 |
11 |
1.571428571 |
2.75 |
3.666666667 |
11 |
6 |
18 |
1.636363636 |
2.571428571 |
4.5 |
6 |
7 |
29 |
1.611111111 |
2.636363636 |
4.142857143 |
7.25 |
8 |
47 |
1.620689655 |
2.611111111 |
4.272727273 |
6.714285714 |
9 |
76 |
1.617021277 |
2.620689655 |
4.222222222 |
6.909090909 |
10 |
123 |
1.618421053 |
2.617021277 |
4.24137931 |
6.833333333 |
11 |
199 |
1.617886179 |
2.618421053 |
4.234042553 |
6.862068966 |
12 |
322 |
1.618090452 |
2.617886179 |
4.236842105 |
6.85106383 |
13 |
521 |
1.618012422 |
2.618090452 |
4.235772358 |
6.855263158 |
14 |
843 |
1.618042226 |
2.618012422 |
4.236180905 |
6.853658537 |
15 |
1364 |
1.618030842 |
2.618042226 |
4.236024845 |
6.854271357 |
16 |
2207 |
1.618035191 |
2.618030842 |
4.236084453 |
6.854037267 |
17 |
3571 |
1.61803353 |
2.618035191 |
4.236061684 |
6.854126679 |
18 |
5778 |
1.618034164 |
2.61803353 |
4.236070381 |
6.854092527 |
19 |
9349 |
1.618033922 |
2.618034164 |
4.236067059 |
6.854105572 |
20 |
15127 |
1.618034014 |
2.618033922 |
4.236068328 |
6.854100589 |
21 |
24476 |
1.618033979 |
2.618034014 |
4.236067844 |
6.854102492 |
22 |
39603 |
1.618033992 |
2.618033979 |
4.236068029 |
6.854101765 |
23 |
64079 |
1.618033987 |
2.618033992 |
4.236067958 |
6.854102043 |
24 |
103682 |
1.618033989 |
2.618033987 |
4.236067985 |
6.854101937 |
25 |
167761 |
1.618033989 |
2.618033989 |
4.236067975 |
6.854101977 |
26 |
271443 |
1.618033989 |
2.618033989 |
4.236067979 |
6.854101962 |
27 |
439204 |
1.618033989 |
2.618033989 |
4.236067977 |
6.854101968 |
28 |
710647 |
1.618033989 |
2.618033989 |
4.236067978 |
6.854101966 |
29 |
1149851 |
1.618033989 |
2.618033989 |
4.236067977 |
6.854101966 |
30 |
1860498 |
1.618033989 |
2.618033989 |
4.236067978 |
6.854101966 |
31 |
3010349 |
1.618033989 |
2.618033989 |
4.236067977 |
6.854101966 |
32 |
4870847 |
1.618033989 |
2.618033989 |
4.236067978 |
6.854101966 |
33 |
7881196 |
1.618033989 |
2.618033989 |
4.236067977 |
6.854101966 |
34 |
12752043 |
1.618033989 |
2.618033989 |
4.236067978 |
6.854101966 |
35 |
20633239 |
1.618033989 |
2.618033989 |
4.236067977 |
6.854101966 |
| |
|
Golden Ratio |
Square
of
Golden Ratio |
Cubic
of
Golden Ratio |
4th power
of
Golden Ratio
|
|
Scatter Plot
of the Ratios |
|
Ratio1
: f(n)/f(n-1) |
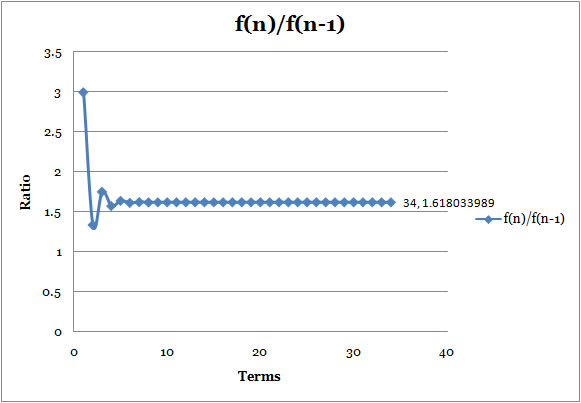
- The first ratio, the ratio of each pair of adjecent terms in the Lucas Sequence, starts differnt number, 3; however, it is still approaching 1.618033989, which is known as Golden Ratio, just like Fibonnaci Sequence.
|
Ratio2
: f(n)/f(n-2) |
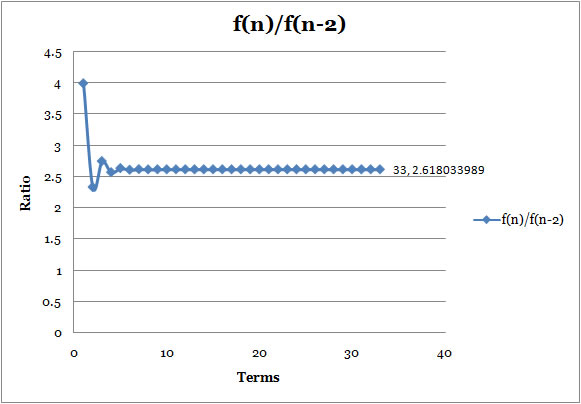
- The second ratio, the ratio of every second term in the Lucas Sequence, starts differnt number, 4; however, it is still approaching 2.618033989, which is square of Golden Ratio, just like Fibonnaci Sequence.
|
Ratio3
: f(n)/f(n-3) |
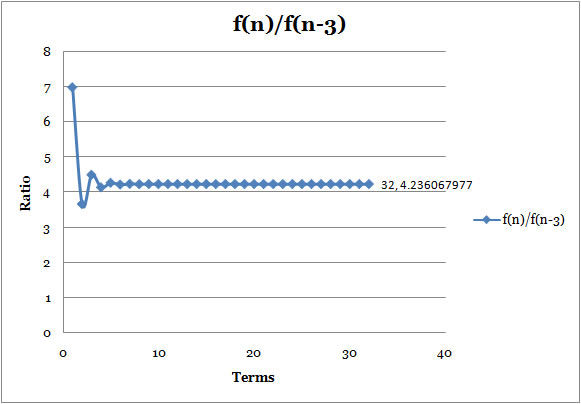
- The third ratio, the ratio of every third term in the Lucas Sequence, starts differnt number, 7; however, it is still approaching 4.236067977, which is cubic of Golden Ratio, just like Fibonnaci Sequence.
|
Ratio4
: f(n)/f(n-4) |
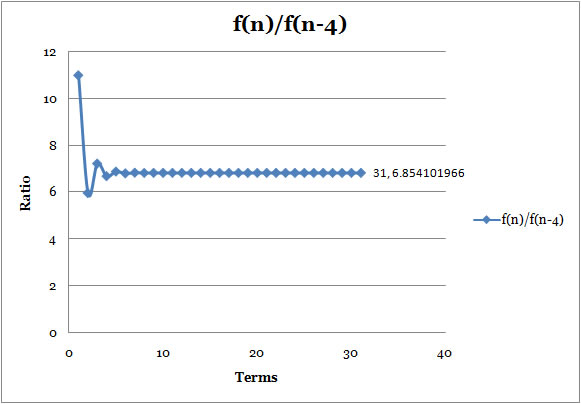
- The forth ratio, the ratio of every forth term in the Lucas Sequence, starts differnt number, 11; however, it is still approaching 6.854101966, which is 4th power of Golden Ratio, just like Fibonnaci Sequence.
|
|
Conclusion |
|
- The Lucas Sequence has different numbers from Fibonnaci Sequence. So, the ratios start from different numbers;
however, they are approaching same limits of the sequence as Fibonnaci Sequence, which are Golden Ratio, Square of Golden Ratio, Cubic Golden Ratio, 4th power of Golden Ratio, etc. respectively.
So, we still can predict that if we calculate f(n)/f(n-5), it would be limited to 5th power of Golden Ratio, and so on, just like Fibonnaci Sequence.
- The first terms of the ratios are same as Lucas Sequence.
So, if we take the first term of each ratio and make a sequence, it would be Lucas Sequence.
|
Back to the Top |
c. Other Sequences
| When
f(0)=1 and f(1)=10
|
|
|
n |
Sequence |
f(n)/f(n-1) |
f(n)/f(n-2) |
f(n)/f(n-3) |
f(n)/f(n-4) |
1 |
1 |
|
|
|
|
2 |
10 |
10 |
|
|
|
3 |
11 |
1.1 |
11 |
|
|
4 |
21 |
1.909090909 |
2.1 |
21 |
|
5 |
32 |
1.523809524 |
2.909090909 |
3.2 |
32 |
6 |
53 |
1.65625 |
2.523809524 |
4.818181818 |
5.3 |
7 |
85 |
1.603773585 |
2.65625 |
4.047619048 |
7.727272727 |
8 |
138 |
1.623529412 |
2.603773585 |
4.3125 |
6.571428571 |
9 |
223 |
1.615942029 |
2.623529412 |
4.20754717 |
6.96875 |
10 |
361 |
1.618834081 |
2.615942029 |
4.247058824 |
6.811320755 |
11 |
584 |
1.617728532 |
2.618834081 |
4.231884058 |
6.870588235 |
12 |
945 |
1.618150685 |
2.617728532 |
4.237668161 |
6.847826087 |
13 |
1529 |
1.617989418 |
2.618150685 |
4.235457064 |
6.856502242 |
14 |
2474 |
1.618051014 |
2.617989418 |
4.23630137 |
6.853185596 |
15 |
4003 |
1.618027486 |
2.618051014 |
4.235978836 |
6.854452055 |
16 |
6477 |
1.618036473 |
2.618027486 |
4.236102027 |
6.853968254 |
17 |
10480 |
1.61803304 |
2.618036473 |
4.236054972 |
6.854153041 |
18 |
16957 |
1.618034351 |
2.61803304 |
4.236072945 |
6.854082458 |
19 |
27437 |
1.61803385 |
2.618034351 |
4.23606608 |
6.854109418 |
20 |
44394 |
1.618034042 |
2.61803385 |
4.236068702 |
6.85409912 |
21 |
71831 |
1.618033969 |
2.618034042 |
4.236067701 |
6.854103053 |
22 |
116225 |
1.618033996 |
2.618033969 |
4.236068083 |
6.854101551 |
23 |
188056 |
1.618033986 |
2.618033996 |
4.236067937 |
6.854102125 |
24 |
304281 |
1.61803399 |
2.618033986 |
4.236067993 |
6.854101906 |
25 |
492337 |
1.618033988 |
2.61803399 |
4.236067972 |
6.854101989 |
26 |
796618 |
1.618033989 |
2.618033988 |
4.23606798 |
6.854101957 |
27 |
1288955 |
1.618033989 |
2.618033989 |
4.236067977 |
6.85410197 |
28 |
2085573 |
1.618033989 |
2.618033989 |
4.236067978 |
6.854101965 |
29 |
3374528 |
1.618033989 |
2.618033989 |
4.236067977 |
6.854101967 |
30 |
5460101 |
1.618033989 |
2.618033989 |
4.236067978 |
6.854101966 |
31 |
8834629 |
1.618033989 |
2.618033989 |
4.236067977 |
6.854101966 |
32 |
14294730 |
1.618033989 |
2.618033989 |
4.236067978 |
6.854101966 |
33 |
23129359 |
1.618033989 |
2.618033989 |
4.236067977 |
6.854101966 |
34 |
37424089 |
1.618033989 |
2.618033989 |
4.236067978 |
6.854101966 |
35 |
60553448 |
1.618033989 |
2.618033989 |
4.236067977 |
6.854101966 |
| |
|
Golden Ratio |
Square
of
Golden Ratio |
Cubic
of
Golden Ratio |
4th power
of
Golden Ratio
|
|
When
f(0)=10 and f(1)=17 |
|
n |
Sequence |
f(n)/f(n-1) |
f(n)/f(n-2) |
f(n)/f(n-3) |
f(n)/f(n-4) |
1 |
10 |
|
|
|
|
2 |
17 |
1.7 |
|
|
|
3 |
27 |
1.588235294 |
2.7 |
|
|
4 |
44 |
1.62962963 |
2.588235294 |
4.4 |
|
5 |
71 |
1.613636364 |
2.62962963 |
4.176470588 |
7.1 |
6 |
115 |
1.61971831 |
2.613636364 |
4.259259259 |
6.764705882 |
7 |
186 |
1.617391304 |
2.61971831 |
4.227272727 |
6.888888889 |
8 |
301 |
1.61827957 |
2.617391304 |
4.23943662 |
6.840909091 |
9 |
487 |
1.617940199 |
2.61827957 |
4.234782609 |
6.85915493 |
10 |
788 |
1.618069815 |
2.617940199 |
4.23655914 |
6.852173913 |
11 |
1275 |
1.618020305 |
2.618069815 |
4.235880399 |
6.85483871 |
12 |
2063 |
1.618039216 |
2.618020305 |
4.23613963 |
6.853820598 |
13 |
3338 |
1.618031992 |
2.618039216 |
4.236040609 |
6.854209446 |
14 |
5401 |
1.618034751 |
2.618031992 |
4.236078431 |
6.854060914 |
15 |
8739 |
1.618033697 |
2.618034751 |
4.236063984 |
6.854117647 |
16 |
14140 |
1.6180341 |
2.618033697 |
4.236069503 |
6.854095977 |
17 |
22879 |
1.618033946 |
2.6180341 |
4.236067395 |
6.854104254 |
18 |
37019 |
1.618034005 |
2.618033946 |
4.2360682 |
6.854101092 |
19 |
59898 |
1.618033983 |
2.618034005 |
4.236067893 |
6.8541023 |
20 |
96917 |
1.618033991 |
2.618033983 |
4.23606801 |
6.854101839 |
21 |
156815 |
1.618033988 |
2.618033991 |
4.236067965 |
6.854102015 |
22 |
253732 |
1.618033989 |
2.618033988 |
4.236067982 |
6.854101948 |
23 |
410547 |
1.618033989 |
2.618033989 |
4.236067976 |
6.854101973 |
24 |
664279 |
1.618033989 |
2.618033989 |
4.236067978 |
6.854101964 |
25 |
1074826 |
1.618033989 |
2.618033989 |
4.236067977 |
6.854101967 |
26 |
1739105 |
1.618033989 |
2.618033989 |
4.236067978 |
6.854101966 |
27 |
2813931 |
1.618033989 |
2.618033989 |
4.236067977 |
6.854101966 |
28 |
4553036 |
1.618033989 |
2.618033989 |
4.236067978 |
6.854101966 |
29 |
7366967 |
1.618033989 |
2.618033989 |
4.236067977 |
6.854101966 |
30 |
11920003 |
1.618033989 |
2.618033989 |
4.236067978 |
6.854101966 |
31 |
19286970 |
1.618033989 |
2.618033989 |
4.236067977 |
6.854101966 |
32 |
31206973 |
1.618033989 |
2.618033989 |
4.236067978 |
6.854101966 |
33 |
50493943 |
1.618033989 |
2.618033989 |
4.236067977 |
6.854101966 |
34 |
81700916 |
1.618033989 |
2.618033989 |
4.236067977 |
6.854101966 |
35 |
132194859 |
1.618033989 |
2.618033989 |
4.236067977 |
6.854101966 |
| |
|
Golden Ratio |
Square
of
Golden Ratio |
Cubic
of
Golden Ratio |
4th power
of
Golden Ratio
|
|
When
f(0)=-7 and f(1)=-3 |
|
n |
Sequence |
f(n)/f(n-1) |
f(n)/f(n-2) |
f(n)/f(n-3) |
f(n)/f(n-4) |
1 |
-7 |
|
|
|
|
2 |
-3 |
0.428571429 |
|
|
|
3 |
-10 |
3.333333333 |
1.428571429 |
|
|
4 |
-13 |
1.3 |
4.333333333 |
1.857142857 |
|
5 |
-23 |
1.769230769 |
2.3 |
7.666666667 |
3.285714286 |
6 |
-36 |
1.565217391 |
2.769230769 |
3.6 |
12 |
7 |
-59 |
1.638888889 |
2.565217391 |
4.538461538 |
5.9 |
8 |
-95 |
1.610169492 |
2.638888889 |
4.130434783 |
7.307692308 |
9 |
-154 |
1.621052632 |
2.610169492 |
4.277777778 |
6.695652174 |
10 |
-249 |
1.616883117 |
2.621052632 |
4.220338983 |
6.916666667 |
11 |
-403 |
1.618473896 |
2.616883117 |
4.242105263 |
6.830508475 |
12 |
-652 |
1.617866005 |
2.618473896 |
4.233766234 |
6.863157895 |
13 |
-1055 |
1.61809816 |
2.617866005 |
4.236947791 |
6.850649351 |
14 |
-1707 |
1.618009479 |
2.61809816 |
4.23573201 |
6.855421687 |
15 |
-2762 |
1.618043351 |
2.618009479 |
4.236196319 |
6.853598015 |
16 |
-4469 |
1.618030413 |
2.618043351 |
4.236018957 |
6.854294479 |
17 |
-7231 |
1.618035355 |
2.618030413 |
4.236086702 |
6.854028436 |
18 |
-11700 |
1.618033467 |
2.618035355 |
4.236060825 |
6.854130053 |
19 |
-18931 |
1.618034188 |
2.618033467 |
4.236070709 |
6.854091238 |
20 |
-30631 |
1.618033913 |
2.618034188 |
4.236066934 |
6.854106064 |
21 |
-49562 |
1.618034018 |
2.618033913 |
4.236068376 |
6.854100401 |
22 |
-80193 |
1.618033978 |
2.618034018 |
4.236067825 |
6.854102564 |
23 |
-129755 |
1.618033993 |
2.618033978 |
4.236068036 |
6.854101738 |
24 |
-209948 |
1.618033987 |
2.618033993 |
4.236067955 |
6.854102053 |
25 |
-339703 |
1.618033989 |
2.618033987 |
4.236067986 |
6.854101933 |
26 |
-549651 |
1.618033989 |
2.618033989 |
4.236067974 |
6.854101979 |
27 |
-889354 |
1.618033989 |
2.618033989 |
4.236067979 |
6.854101961 |
28 |
-1439005 |
1.618033989 |
2.618033989 |
4.236067977 |
6.854101968 |
29 |
-2328359 |
1.618033989 |
2.618033989 |
4.236067978 |
6.854101966 |
30 |
-3767364 |
1.618033989 |
2.618033989 |
4.236067977 |
6.854101967 |
31 |
-6095723 |
1.618033989 |
2.618033989 |
4.236067978 |
6.854101966 |
32 |
-9863087 |
1.618033989 |
2.618033989 |
4.236067977 |
6.854101966 |
33 |
-15958810 |
1.618033989 |
2.618033989 |
4.236067978 |
6.854101966 |
34 |
-25821897 |
1.618033989 |
2.618033989 |
4.236067977 |
6.854101966 |
35 |
-41780707 |
1.618033989 |
2.618033989 |
4.236067978 |
6.854101966 |
| |
|
Golden Ratio |
Square
of
Golden Ratio |
Cubic
of
Golden Ratio |
4th power
of
Golden Ratio
|
|
Conclusion |
|
- As we see, no matter what numbers we put into f(0) and f(1), the ratios are approaching the same limits of the sequence as Fibonnaci Sequence, which are Golden Ratio, Square of Golden Ratio, Cubic Golden Ratio, 4th power of Golden Ratio, etc. respectively.
>>> Conjecture : The reason why the ratios are approaching the same limits of the sequence as Fibonnaci Sequence, which are Golden Ratio, Square of Golden Ratio, Cubic Golden Ratio, 4th power of Golden Ratio, etc. respectively, is the ratios come from the recursion, not from the initial numbers.
|
|
 Go Back to Top Go Back to Top |
 Go
Back to Michelle's Main page Go
Back to Michelle's Main page |
 Go
Back to EMAT 6680 Homepage Go
Back to EMAT 6680 Homepage |
Copyright
@ Michelle E. Chung |
|