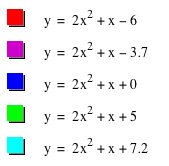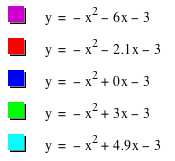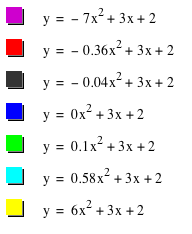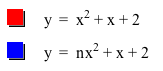|
Michelle E. Chung |
*
EMAT6680 Assignment 2: Parabolas |
|
1. Construct graphs for the parabola
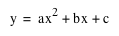
for different values of a, b, and c. (a, b, c can be any rational numbers.)
|
 |
|
Graph of
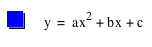
|
|
|
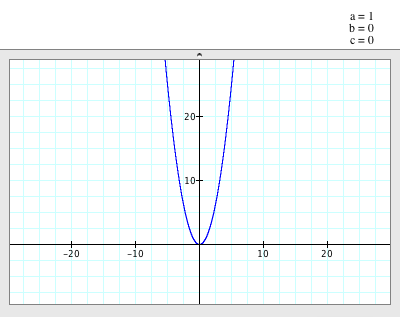
As
we know, this is the simplest parabola graph, which is 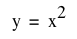 . .
- The parabola
opens up.
- The vertex
of the parabola is (0,0).
- The axis
of symmetry is x=0.
|
When
a=b=c=1
(a,b,c>0) |
|
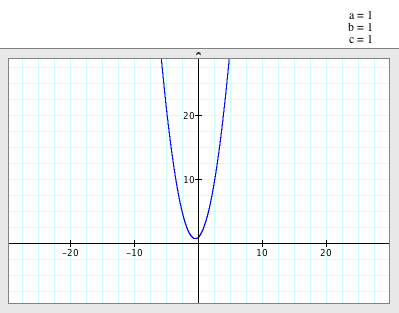
When
a=b=c=1,
-
The parabola opens up.
- The
vertex of the parabola is (-1/2, 3/4).
- The
axis of symmetry is x=- 1/2.
|
|
When a=c=1, b=3
(a,b,c>0)
|
|
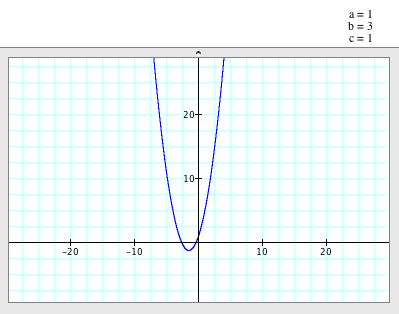
When
a=c=1 and b=3,
-
The parabola opens up.
- The
vertex of the parabola is (-3/2, -5/4).
- The
axis of symmetry is x=- 3/2.
|
|
When a=c=1, b=-3
(a,c>0 & b<0) |
|
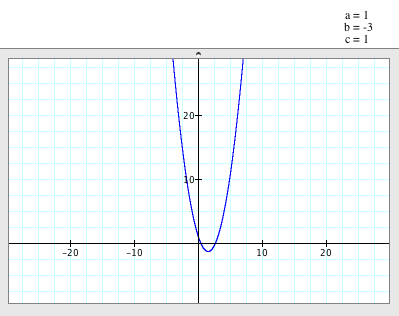
When
a=c=1 and b=-3,
- The parabola opens up.
- The
vertex of the parabola is (3/2, -5/4).
- The
axis of symmetry is x= 3/2.
|
When a=1, b=5, c=-4
(a,b>0 & c<0) |
|
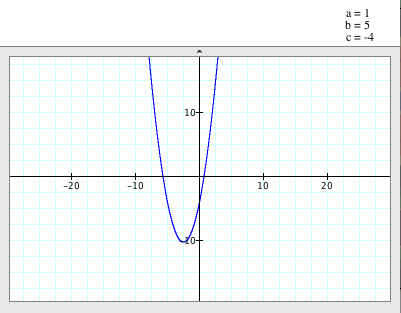
When
a=1, b=3 and c=-4,
- The parabola opens up.
- The
vertex of the parabola is (-5/2, -41/4).
- The
axis of symmetry is x=- 5/2.
|
When
a=-0.3, b=5, c=5.3
(a<0 & b,c<0) |
|
|
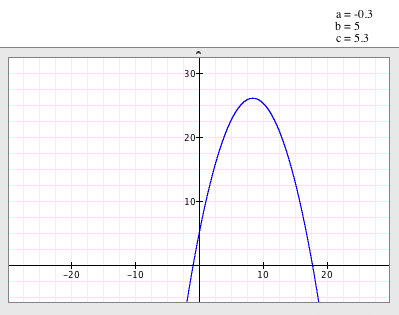
When
a=-0.3, b=5 and c=5.3,
- The parabola opens down.
- The
vertex of the parabola is (25/3, 339/5).
- The
axis of symmetry is x= 25/3.
|
When
a=-0.3, b=-7.8, c=-2
(a,b,c<0) |
|
|
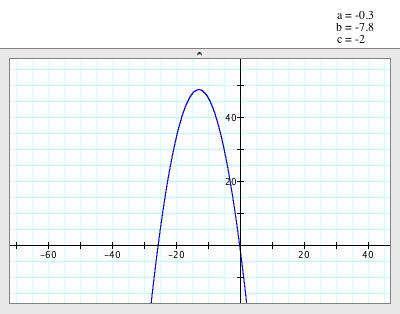
When
a=-0.3, b=-7.8 and c=-2,
- The parabola opens down.
- The
vertex of the parabola is (-13, 48.7).
- The
axis of symmetry is x= -13.
|
Back to the Top |
|
2. Fix two of the values for a, b, and c. Make at least 5 graphs on the same axes
as you vary the third value.
How do you change the equations to explore other graph?
|
 |
Graph of
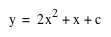
when c varies:
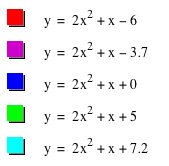
|
|
|
As you see,
'c' is y-intercept of the graph.
- As c increases, the graph moves up.
- As c decreases, the graph moves down.
|
Graph of
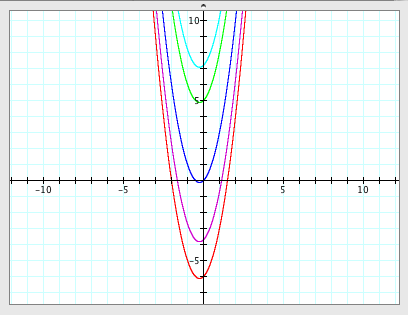
when b varies:
|
|
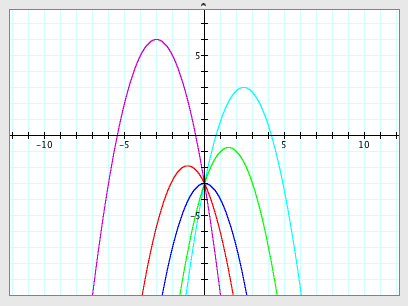
As you see,
'b' determines x-coordinate of the vertex of the graph with a.
- As b increases, the graph moves to the right.
- As b decreases, the graph moves to the left.
|
| Graph of
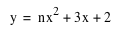
when a varies:
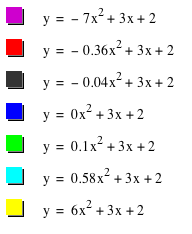
|
|
As you see,
'a' determines whether the graph opens up or opens down and also determines the width of the graph.
- If a is positive, the graph opens up.
- If a is negative, the graph opens down.
- As |a| increases, the graph is getting thinner.
- As |a| decreases, the graph is getting wider.
|
| Conclusion |
- 'a' determines whether the graph opens up or opens down and also determines the width of the graph.
- If a is positive, the graph opens up, and if a is negative, the graph opens down.
- As |a| increases, the graph is getting thinner, and as |a| decreases, the graph is getting wider.
- 'b' determines x-coordinate of the vertex of the graph with 'a'.
- As b increases, the graph moves to the right, and as b decreases, the graph moves to the left.
- 'c' is y-intercept of the graph.
- As c increases, the graph moves up, and as c decreases, the graph moves down.
|
Back to the Top |
4. Interpret your graphs. What happens to
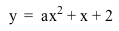
(i.e. the case where b=1 and c=2) as a is varied?
Is there a common point to all graphs? What is it?
What is the significance of the graph where a=0?
Do the similar interpretations for other sets of graphs.
How does the shape change?
How does the position change?
|
 |
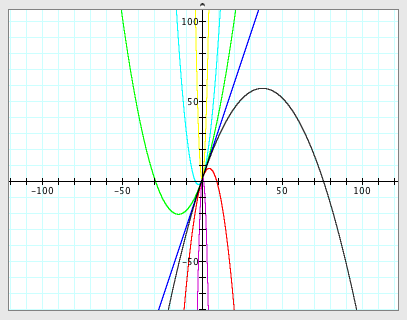
Graphs of
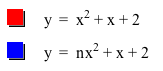
when n is in [-10, 10] |
|
|
|
The common point
to all graphs |
|
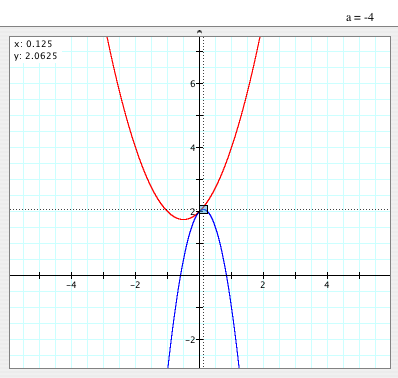
- These are the graphs of
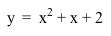 and and 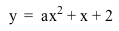 when a=-4. when a=-4.
- The vertex of the graph of
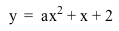 is (0.125, 2.0625). is (0.125, 2.0625).
- Since |a| is 4 and is greater than 1, it is thinner than
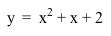 . .
- Both graphs pass (0, 2).
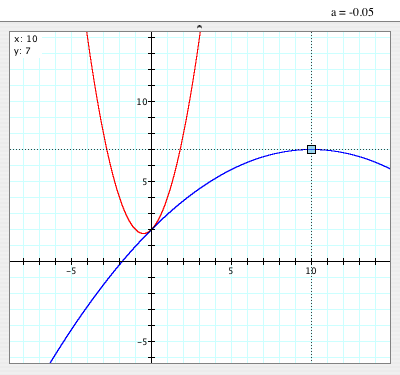
- These are the graphs of
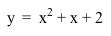 and and 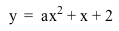 when a=-0.05. when a=-0.05.
- The vertex of the graph of
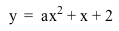 is (10, 7). is (10, 7).
- Since |a| is 0.05 and is less than 1, it is wider than
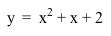 . .
- Both graphs pass (0, 2).
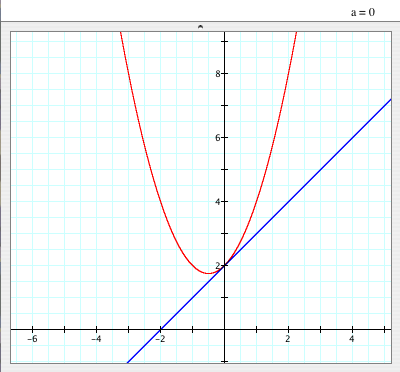
- These are the graphs of
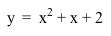 and and 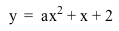 when a=0. when a=0.
- There is no vertex because the graph of
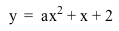 is a straight line. is a straight line.
- Both graphs pass (0, 2).
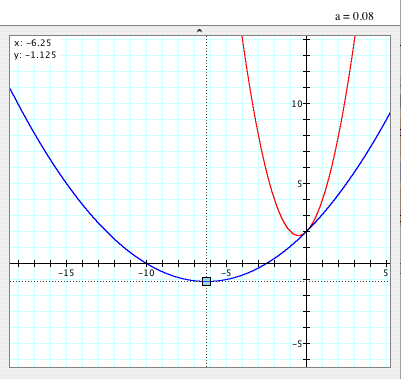
- These are the graphs of
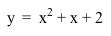 and and 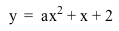 when a=0.08. when a=0.08.
- The vertex of the graph of
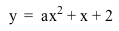 is (-6.25, -1.125). is (-6.25, -1.125).
- Since |a| is 0.08 and is less than 1, it is wider than
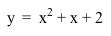 . .
- Both graphs pass (0, 2).
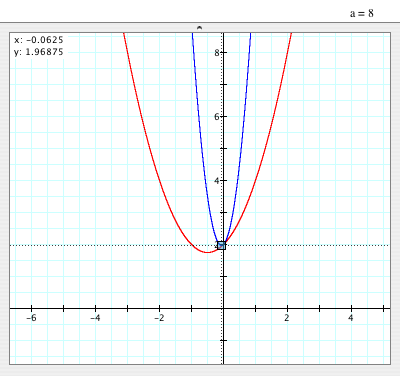
- These are the graphs of
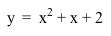 and and 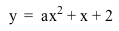 when a=8. when a=8.
- The vertex of the graph of
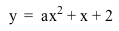 is (-0.0625, 1.96875). is (-0.0625, 1.96875).
- Since |a| is 8 and is greater than 1, it is thinner than
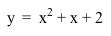 . .
- Both graphs pass (0, 2).
|
|
The siginificance
of the graph
where a=0? |
|

- These are the graphs of
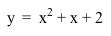 and and 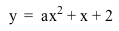 when a=0. when a=0.
- When a=0, the graph of
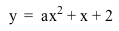 is a straight line because the equation would be y=bx+c, which is a linear equation. is a straight line because the equation would be y=bx+c, which is a linear equation.
So, to be a parabola, 'a' should not be '0'; otherwise, it would be a straight line.
- Even though the graph is a straight line, the graph of
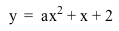 when a=0 still passes (0, 2). when a=0 still passes (0, 2).
|
| Conclusion |
|
- 'a' determines whether the graph opens up or opens down and also determines the width of the graph.
- If 'a' is positive, the graph opens up.
- If 'a' is negative, the graph opens down.
- When |a| increases, the graph is getting thinner.
- When |a| decreases, the graph is getting wider.
- When a=0, the graph is a straight line because y=bx+c, which is a linear equation.
- Since c is y-intercept, the graph always passes (0, 2). So, (0, 2) is the common point of the graphs.
|
|
 Go Back to Top Go Back to Top |
 Go
Back to Michelle's Main page
Go
Back to Michelle's Main page |
 Go
Back to EMAT 6680 Homepage
Go
Back to EMAT 6680 Homepage |
Copyright
@ Michelle E. Chung |