Logo

 Michelle E. Chung
* EMAT6680 Assignment 4: Centers of a Triangle

INCENTER(I)

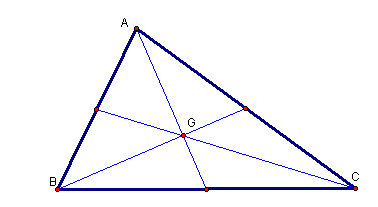
1. The CENTROID(G) of a triangle is the common intersection of the three medians.
    A median of a triangle is the segment from a vertex to the midpoint of the opposite side.
    Let's construct the Centroid using Geometer's Sketchpad (GSP) and explore its location for various shapes.
 
Steps for constructing    

Given:

Point A, Point B, Point C

Stpes:

  1. Let AB = segment between A and B.
  2. Let BC = segment between B and C.
  3. Let CA = segment between C and A.
  4. Let E = midpoint of AB.
  5. Let EC = line through midpoint E and point C.
  6. Let F = midpoint of BC.
  7. Let FA = line through midpoint D and point B.
  8. Let D = midpoint of CA.
  9. Let DB = line through midpoint D and point B.
  10. Let "G(Centroind)" = intersection of DB and EC.
Picture   Centroid
Location  
Acute Triangle The centroid of a acute triangle is inside of the triangle. Centroid of Acute triangle
Right Triangle The centroid of a right triangle is inside of the triangle. Centroid of Right triangle
Obtuse Triangle The centroid of a obtuse triangle is inside of the triangle. Centroid of Obtuse triangle
* The centroid of a triangle is always inside of the triangle, and it moves along a line segment side to side.
 Centroid of triangle Movie

Back to the Top

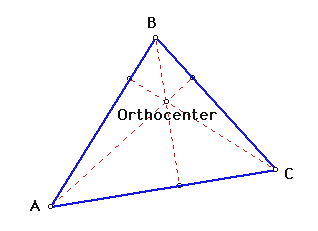
2. The ORTHOCENTER(H) of a triangle is the common intersection of the three lines containig the altitudes.
    An altitude is a perpendicular segment from a vertex to the line of the opposite side.
    (Note: the foot of the perpendicular may be on the extention of the side of the triangle.)
    It should be on clear that H does not have to be on the segments that are the altitudes.
    Rather, H lies on the lines extended along the altitudes.
 
Steps for constructing    

Given:

Point A, Point B, Point C

Stpes:

  1. Let AB = segment between A and B.
  2. Let BC = segment between B and C.
  3. Let CA = segment between C and A.
  4. Let l = line perpendicular to AB passing through C.
  5. Let j = line perpendicular to CA passing through B.
  6. Let k = line perpendicular to BC passing throuhg A.
  7. Let FA = line through midpoint D and point B.
  8. Let "H(Orthocenter)" = intersection of perpendicular line j and perpendicular line k.
Picture   Orthocenter
Location  
Acute Triangle The orthocenter of a acute triangle is inside of the triangle. Orthocenter of Acute triangle
Right Triangle The orthocenter of a right triangle lies on the intersection of two sides (not hypotenuse). Orthocenter of Right triangle
Obtuse Triangle The orthocenter of a obtuse triangle is outside of the triangle. Orthocenter of Obtuse triangle
* The orthocenter of a triangle is inside, on , or outside of the triangle, and it moves along an arc that passes through two vertices of the side of the triangle.
 Orthocenter of triangle Movie

Back to the Top

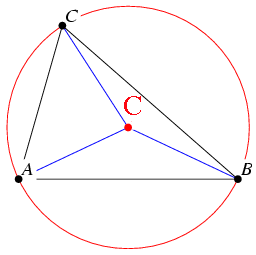
3. The CIRCUMCENTER(C) of a triangle is the point in the plane equidistant from the three vertices of the triangle.
    Since a point equidistance from two points lies on the perpendicular bisector of the segment determined by the two points,
    C is on the perpendicular bisector of each side if the triangle.
    (Note: C may be outside of the triangle.)
    Also, it is the center of the CIRCUMCIRCLE(the circumscribed circle) of the triangle.
 
Steps for constructing    

Given:

Point A, Point B, Point C

Stpes:

  1. Let CA = segment between C and A.
  2. Let AB = segment between A and B.
  3. Let BC = segment between B and C.
  4. Let D = midpoint of CA.
  5. Let l = line perpendicular to CA passing through D.
  6. Let E = midpoint of AB.
  7. Let j = line perpendicular to AB passing through E.
  8. Let F = midpoint of BC.
  9. Let k = line perpendicular to BC passing through F.
  10. Let "C(Circumcenter)" = intersection of perpendicular line j and perpendicular line k.
Picture   Circumcenter
Location  
Acute Triangle The circumcenter of a acute triangle is inside, on, or outside of the triangle. Orthocenter of Acute triangle
Right Triangle The circumcenter of a right triangle lies exactly at the midpoint of the hypotenuse (longest side). Orthocenter of RIght triangle
Obtuse Triangle The circumcenter of a obtuse triangle is always outside of the triangle. Orthocenter of Obtuse triangle

* The circumcenter of a triangle is inside, on , or outside of the triangle, and it moves up and down.

 Orthocenter of triangle Movie

Back to the Top

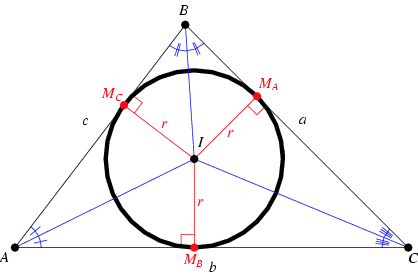
4. The INCENTER(I) of a triangle is the point on the interior of the triangle that is equidistant from the three sides.
    Since a point interior to an angle that is equidistant from two sides of the angle lies on the angle bisector,
    I must be on the angle bisector of each angle of the triangle.
   Also, it is the center of the INCIRCLE(the inscribed circle) of the triangle.
 
Steps for constructing    

Given:

Point A, Point B, Point C

Stpes:

  1. Let AB = segment between A and B.
  2. Let BC = segment between B and C.
  3. Let CA = segment between C and A.
  4. Let l = ray bisecting angle C-A-B.
  5. Let j = ray bisecting angle A-B-C.
  6. Let k = ray bisecting angle B-C-A.
  7. Let "I(Incenter)" = intersection of bisector j and bisector k.
Picture   Incenter
Location  
Acute Triangle The incenter of a acute triangle is inside of the triangle. Incenter of Acute triangle
Right Triangle The incenter of a right triangle is inside of the triangle. Incenter of Right triangle
Obtuse Triangle The incenter of a obtuse triangle is inside of the triangle. Incenter of Obtuse triangle

* The incenter of a triangle is always inside of the triangle, and it moves along a curved line side to side.

 Incenter of triangle Movie

Back to the Top

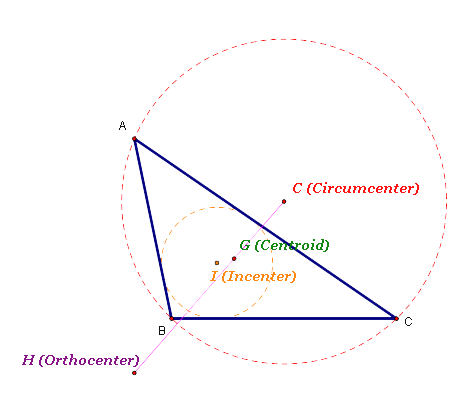
5. Use GSP to construct G, H, C, and I for the same triangle.
    What relationships can you find among G, H, C, and I or subsets of them?
 
Picture    

Centers

 
Location  
Acute Triangle The four centers of a acute triangle is inside, on, or outside of the triangle, and all of them could be on the same line. Centers of Acute triangle
Right Triangle Only Orthocenter, Centroid, and Circumcenter are on the same line. Centers of Right triangle
Obtuse Triangle The four centers of a acute triangle is inside or outside of the triangle, and all of them could be on the same line. Centers of Obtuse triangle

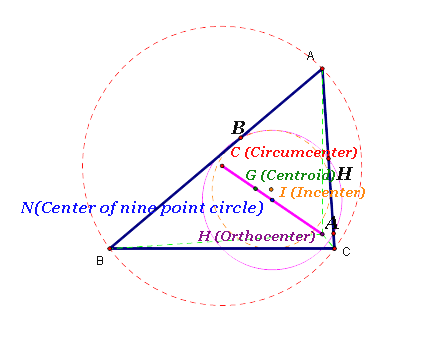
* The centers of a triangle is inside, on, or outside of the triangle, and orthocenter, centroid, and circumcenter are always on the same line, which is called 'Euler Line'.

Centers of triangle Movie

* On Euler line, there are Center of nine point circle, Circumcenter, Centroid, and Orthocenter. Also, the nine point circle exsits only on acute triangles.
EulerLine

 

 
Button Go Back to Top
Button Go Back to Michelle's Main page
Button Go Back to EMAT 6680 Homepage
Copyright @ Michelle E. Chung