Logo

 Michelle E. Chung
* EMAT6680 Assignment 7: Tangent Circles
Tangent Circle
when circle B is
outside of circle A

 

Given two circles and a point on one of the circles.
Construct a circle tangent to the two circles with one point of tangency being the designated point.
Seperator3


1. When circle B is outside of the tangent circle C

 
Construction    

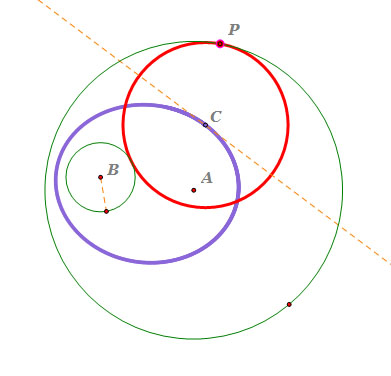
TangentCircle

  • Circle C is the tangent circle of circle A and circle B.
    As we see, the tangent circle C is inscribed to circle A and is circumscribed to circle B.
  • Locus of the center C is an ellipse, and the orange line is the tangent line of the locus.
Script   Please click here for GSP animation of the Tangent Circle when circle B is outside of it
>>>TANGENT CIRCLE SCRIPT when circle B is outside of it
Reference  

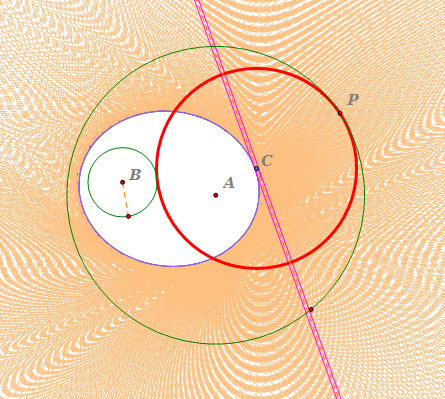
Envelope2    Envelope

  • If we move point P along the circle A,
    we can get the locus of the center of the tangent circle, which is an ellipse, and an envelope of lines is produced all tangent to the ellipse.

Back to the Top


2. When circle B is inside of the tangent circle C

 
Construction    

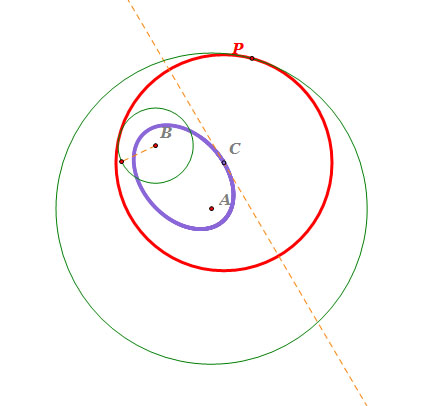
TangentCircle_Bin

  • Circle C is the tangent circle of circle A and circle B.
    As we see, the tangent circle C is inscribed to circle A and is circumscribed to circle B;
    however, circle B is inside of the tangent circle.
  • Locus of the center C is an ellipse, and the orange line is the tangent line of the locus.
Script   Please click here for GSP animation of the Tangent Circle when circle B is inside of it
>>>TANGENT CIRCLE SCRIPT when circle B is inside of it
Reference  

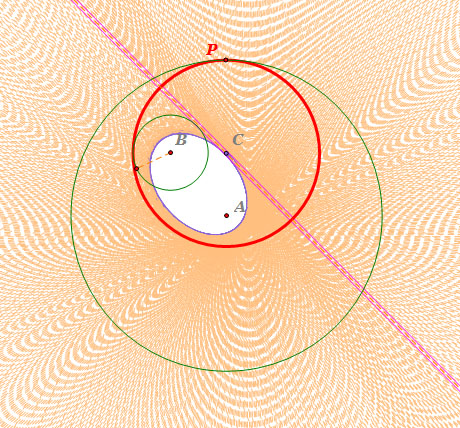
Envelope_Bin    Envelope

  • If we move point P along the circle A,
    we can get the locus of the center of the tangent circle, which is an ellipse, and an envelope of lines is produced all tangent to the ellipse.

Back to the Top


3. When circle A and circle B intersect

 
Construction    

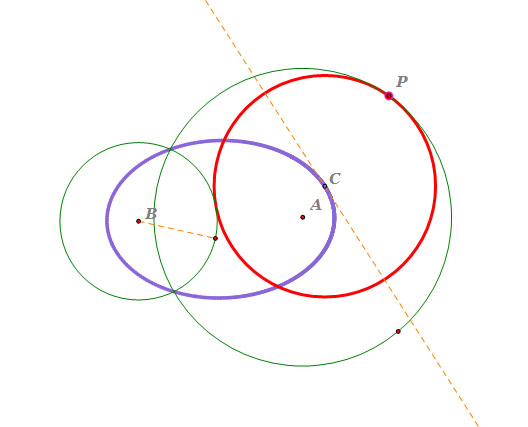
TangentCircle_Intersect

  • Circle C is the tangent circle of circle A and circle B.
    As we see, the tangent circle C is inscribed to circle A and is circumscribed to circle B;
    however, circle A and circle B are intersecting.
  • Locus of the center C is an ellipse, and the orange line is the tangent line of the locus.
Script   Please click here for GSP animation of the Tangent Circle when circle A and circle B intesect
>>>TANGENT CIRCLE SCRIPT when circle A and circle B intersect (circumscribed)
Reference  

TangentCircle_Intersect

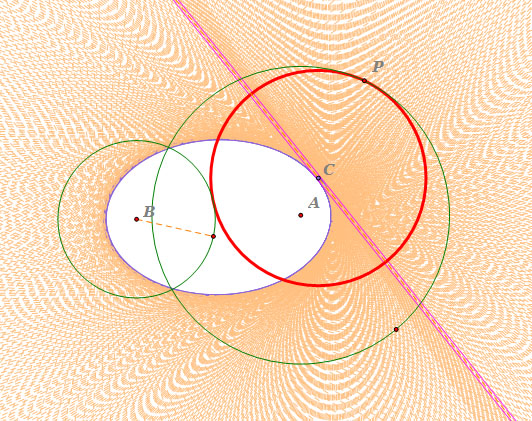
Envelope

  • If we move point P along the circle A,
    we can get the locus of the center of the tangent circle, which is an ellipse, and an envelope of lines is produced all tangent to the ellipse.

Back to the Top


4. When circle B is outside of circle A

 
Construction    

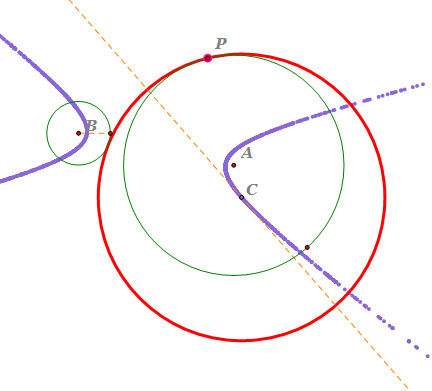
TangentCircle_BoutA

  • Circle C is the tangent circle of circle A and circle B.
    As we see, the tangent circle C iscircumscribed to circle A and circle B.
    Also, circle B is outside of circle A and there are apart.
  • Locus of the center C is a hyperbola, and the orange line is the tangent line of the locus.
Script   Please click here for GSP animation of the Tangent Circle when circle B is outside of circle A
>>>TANGENT CIRCLE SCRIPT when circle B is outside of circle A
Reference    

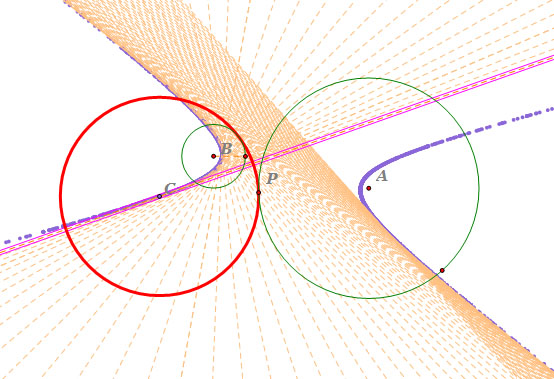
Envelope_BoutA

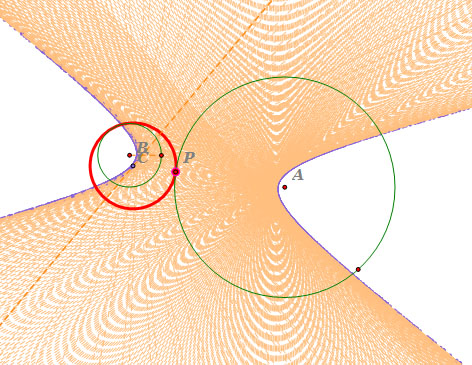
Envelope2_BoutA

  • If we move point P along the circle A,
    we can get the locus of the center of the tangent circle, which is a hyperbola, and an envelope of lines is produced all tangent to the hyperbola.

Back to the Top


5. Tangent Circle Movie

 
Tangent Circle Movie    

Please click here for GSP animation of the Tangent Circle Movie
>>>TANGENT CIRCLE Movie SCRIPT
Construction  

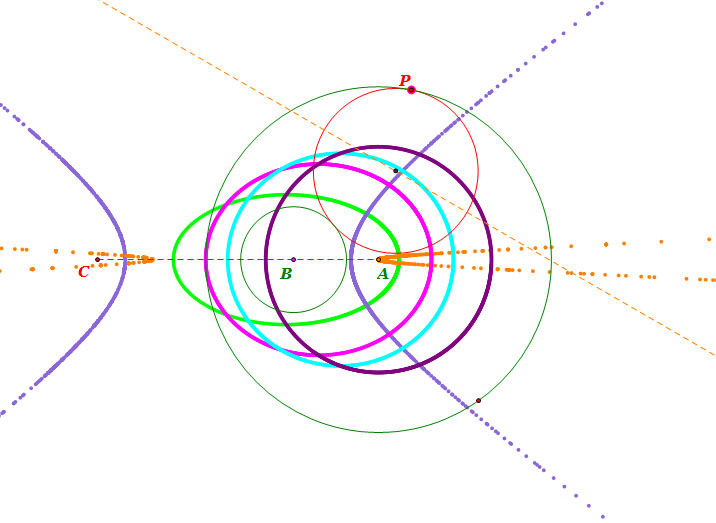
TangentCircle

  • When centers of circle A and circle B are on the same position, the locus of the tangent circle is a circle.
  • When circle B is inside of circle A, the locus of the tangent circle is an ellipse.
  • When circle B is inscribed to circle A, the locus of the tangent circle is an ellipse, too, and the ellipse is also inscribed to circle A.
  • When circle A and circle B intersect, the locus of the tangent circle is an ellipse, too.
  • When circle B is circumscribed to circle A, the locus of the tangent circle is a hyperbola.
  • When circle B is outside of circle A, the locus of the tangent circle is a hyperbola, too.

Conjecture  

The locus of tangent circle of two circles is one of the conic, except a parabola.
Proof  

1. Ellipse

When circle B is inside of circle A

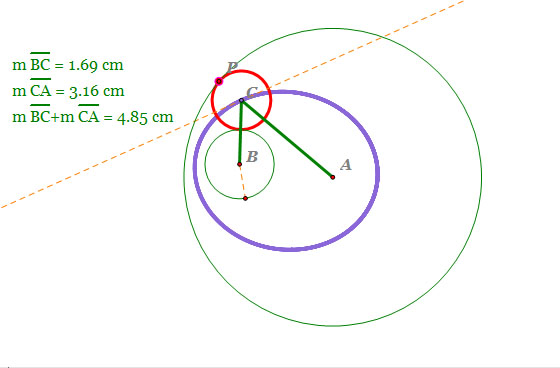
Ellipse1

  • Center A and B are faci of the ellipse.
  • m(line segment AC) + m(line segment BC) = constant
  • Note that the sum of line segment AC and line segment BC is constant.
    So, by the definition of an ellipse, the locus of the center of tangent circle is an ellipse.

Please click here for GSP animation of the Ellipse Movie_BinsideA
>>> Ellipse Movie SCRIPT when circle B is inside of circle A
When circle A and circle B intersect

Ellipse2

  • Center A and B are faci of the ellipse.
  • m(line segment AC) + m(line segment BC) = constant
  • Note that the sum of line segment AC and line segment BC is constant.
    So, by the definition of an ellipse, the locus of the center of tangent circle is an ellipse.
Please click here for GSP animation of the Ellipse Movie_ABintersect
>>> Ellipse Movie SCRIPT when circle A and circle B intersect
When circle B is inscribed to circle A

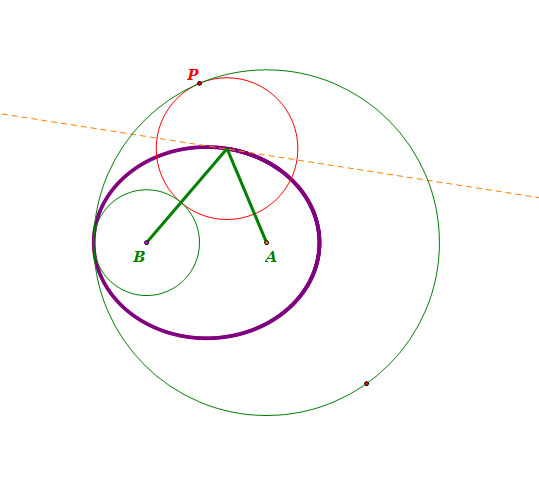
Ellipse3

  • Center A and B are faci of the ellipse.
  • m(line segment AC) + m(line segment BC) = constant
  • Note that the sum of line segment AC and line segment BC is constant.
    So, by the definition of an ellipse, the locus of the center of tangent circle is an ellipse
Please click here for GSP animation of the Ellipse Movie_BinscribedA
>>> Ellipse Movie SCRIPT when circle B is inscribed to circle A

 

2. Hyperbola

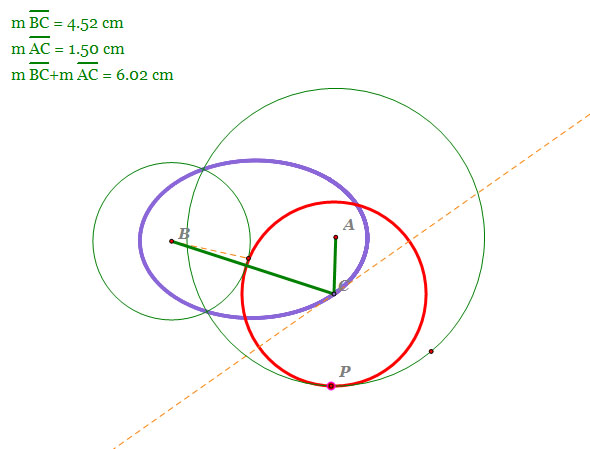
When circle B is circumscribed to circle A

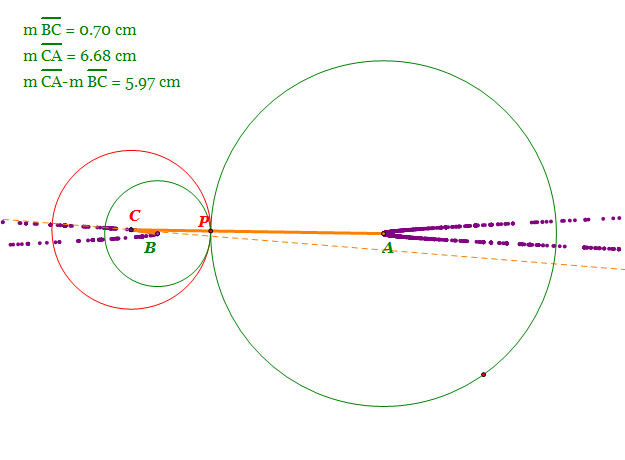
Hyperbola1

  • Center A and B are foci of the hyperbola.
  • | m(line segment AC) - m(line segment BC) |= constant
  • Note that the differnce of line segment AC and line segment BC is constant.
    So, by the definition of a hyperbola, the locus of the center of tangent circle is a hyperbola.

Please click here for GSP animation of the Ellipse Movie_BcircumscribedA
>>> Ellipse Movie SCRIPT when circle B is circumscribed to circle A
When circle B is outside of circle A

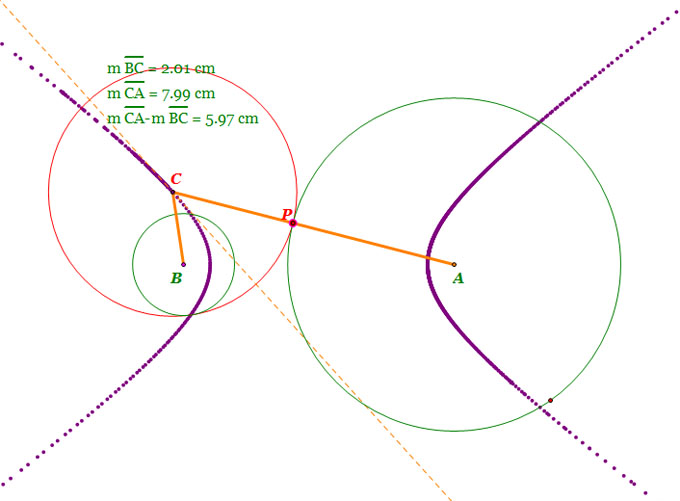
Hyperbola2

  • Center A and B are foci of the hyperbola.
  • | m(line segment AC) - m(line segment BC) |= constant
  • Note that the differnce of line segment AC and line segment BC is constant.
    So, by the definition of a hyperbola, the locus of the center of tangent circle is a hyperbola.
Please click here for GSP animation of the Ellipse Movie_ABintersect
>>> Ellipse Movie SCRIPT when circle A and circle B intersect


 

3. Circle

When circle A and circle B have the same center

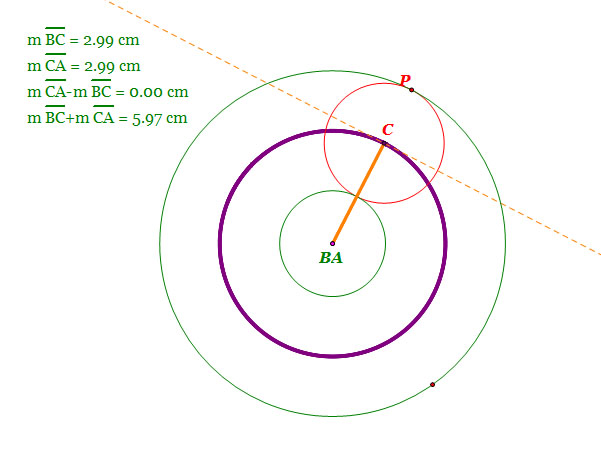
Circle

  • Center A and B are same point here, and they are the center of the tangent circle.
  • | m(line segment AC) - m(line segment BC) |= 0
  • m(line segment AC) + m(line segment BC) = constant
  • Note that the distance between center A(B) and center C is constant, which is a radius.
    So, by the definition of a circle, the locus of the center of tangent circle is a circle.

Please click here for GSP animation of the Ellipse Movie_ABsamecenter
>>> Ellipse Movie SCRIPT when circle A and circle B have the same center


 
Button Go Back to Top
Button Go Back to Michelle's Main page
Button Go Back to EMAT 6680 Homepage
Copyright @ Michelle E. Chung