Logo

 Michelle E. Chung
* EMAT6680 Assignment 9: Pedal Triangles
Pedal Triangle Proof
Simson Line by Angle

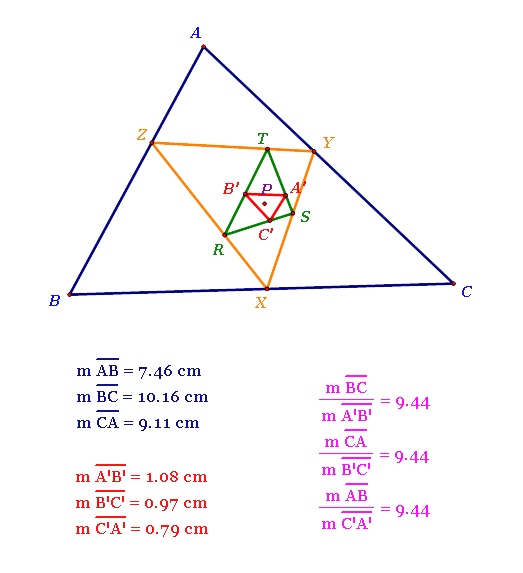
1c. Prove the pedal triangle of the pedal triangle of the pedal triangle of a point is similar to the original triangle.
      That is, show that the pedal triangle A'B'C' of pedal triangle RST of the pedal triangle XYZ of pedal point P is similar to triangle ABC.

 
Construction     PedalOfPedalOfPedalTri
Proof  

Look at the construction above.

It is kind of hard to prove this statement... so I used GSP.
Believe it or not, triangle ABC and triangle A'B'C' are similar since ratios of corresponding sides are congruent.

Also, line segments AB and C'A', line segments BC and A'B', and line segments CA and B'C' are corresponding sides respectively.
 

Back to the Top

9. Find all conditions in which the three vertices of the Pedal triangle are colinear (that is, it is a degenerate triangle).
    This line segment is called the Simson Line.

 
Construction    

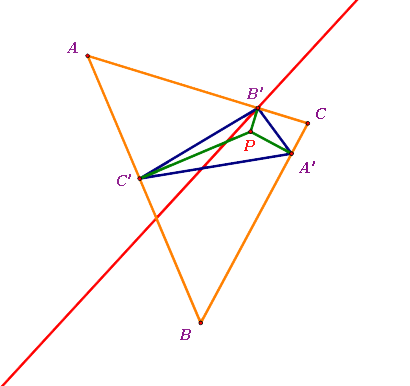
Before putting vertices on the Simson Line

: Triangle ABC is the original triangle and triangle A'B'C' is the pedal triangle for pedal point P.

- As you see, P is inside of the original triangle.

 Pedal_Before_Simson

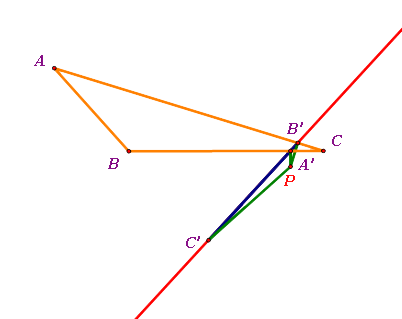
When three vertices on the Simson Line

: If we move the vertices of the pedal triangle to the line, which is called the Simson Line, the original triangle moves to the other side of the line and now P is outside of the original triangle.

 

 OnSimonLine

Back to the Top
Cases by Position

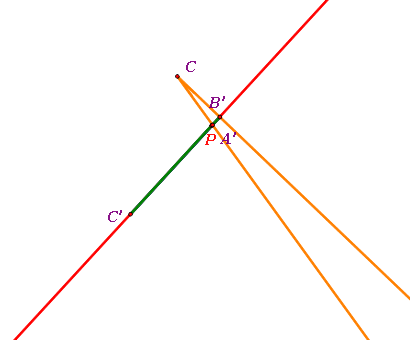
When P is on the triangle

: If P is on the side of the original triangle, the original triangle would be very long shape, but it is still a triangle.

 PonTri

When P is outside of the triangle

  • When the pedal point P is near by the Simson Line
    - The pedal point P and the original triangle ABC seem to be on the opposite sides of the Simson Line.
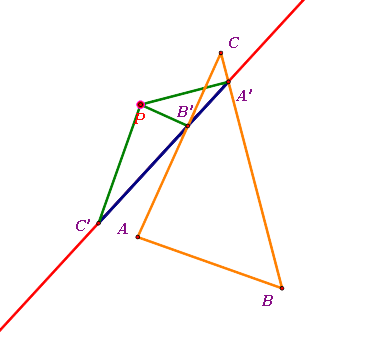 PoutsideTri
  • When the pedal point P is farther from the Simson Line
    - The pedal point P and the original triangle ABC seem to be on the same side of the Simson Line.
    - The original triangle ABC seems to be apart from the Simson Line.
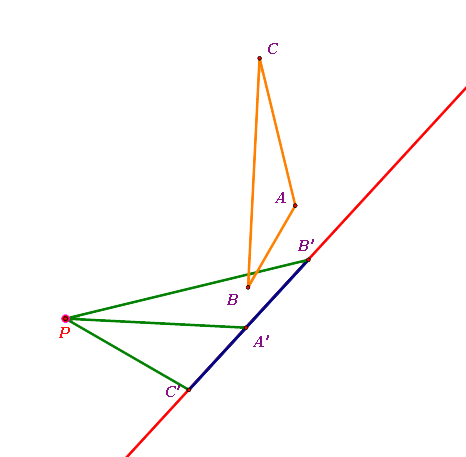 PoutsideTri2
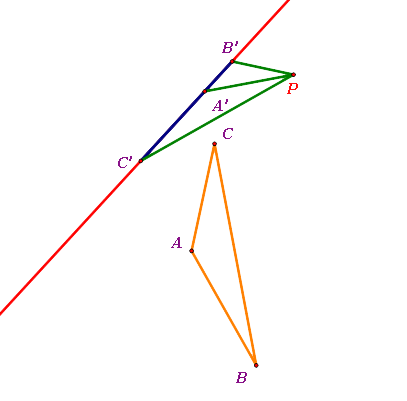PoutsideTri3

Back to the Top
Cases by Angle

When m(angle PA'B') is an acute angle

  • The original triangle ABC is on the LEFT side of the pedal point P.
  • The original triangle ABC is on or apart from the Simson Line.
 PAcute
PAcute2

When m(angle PA'B') is a right angle

  • The base of the original triangle ABC is on the Simson Line, and it is congruent to the base of the pedal triangle A'B'C'.
  • The pedal point P and the original triangle are on the opposite sides.
  • Two perpendicular lines from the pedal point P and the vertex of the original triangle A to the Simson Line are parallel.
 PRight

When m(angle PA'B') is an obtuse angle

  • The original triangle ABC is on the RIGHT side of the pedal point P.
  • The original triangle ABC is on or apart from the Simson Line.
 PObtuse
PObtuse2

 
Conclusion

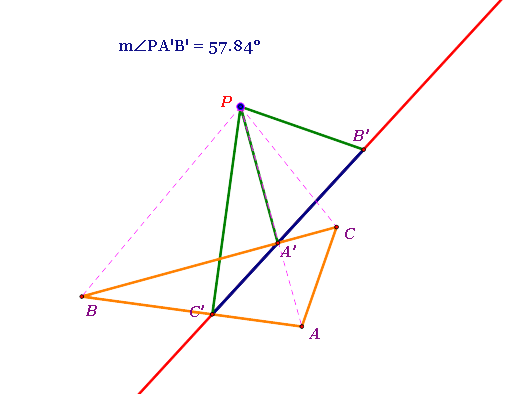
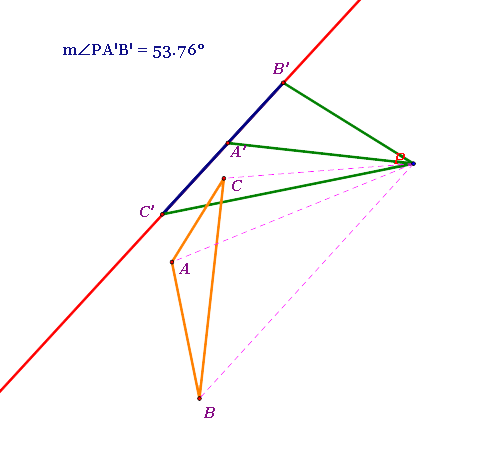
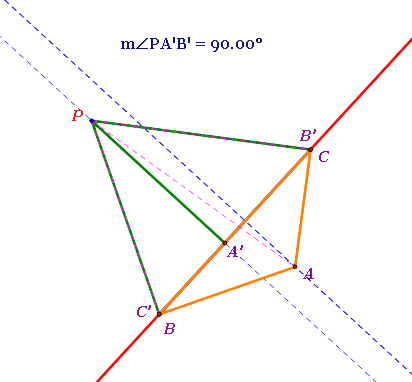
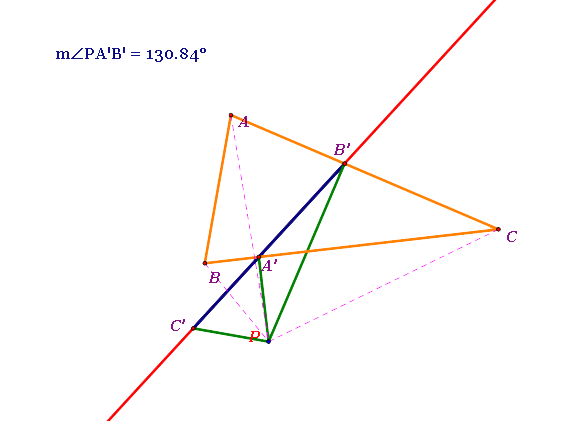
From the observation, the position of the original triangle ABC seems to be determined by the angle PA'B', not by the position of the pedal point P.

  • When m(angle PA'B') is an ACUTE angle, the original triangle ABC is on the LEFT side of the pedal point P and is on or apart from the Simson Line.
  • When m(angle PA'B') is a RIGHT angle, the base of the original triangle ABC is on the Simson Line and the altitudes from the pedal point P and the vertex A are parallel.
  • When m(angle PA'B') is an OBTUSE angle, the original triangle ABC is on the RIGHT side of the pedal point P and is on or apart from the Simson Line.

 
Button Go Back to Top
Button Go Back to Michelle's Main page
Button Go Back to EMAT 6680 Homepage
Copyright @ Michelle E. Chung