Quadratics
in the xb-plane
By Courtney
Cody
Consider the following
equation:
This equation is the special case
of the general quadratic equation 
, where a=1, c=1, and b
is some constant. In this
exploration, we will look at the effect b has on the equation 
by studying the
graph of the equation and investigating what happens when the value b is varied.
LetŐs start by graphing this equation in the xb-plane and seeing what we get. To graph in the xb-plane, we simply graph and substitute y in for b
so that now b becomes a
variable. Hence, we get the
following graph:
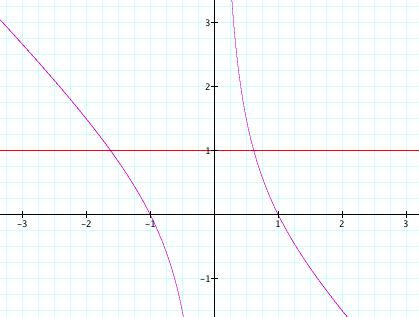
Graph A
When 
is graphed in the xb-plane, we notice that it is a hyperbola. If we take any particular value of b, say b =
4, and overlay this equation on the graph we are actually adding a line
parallel to the x-axis. This is because
we have allowed b to be an axis on
our graph. In particular, b is represented as the y-axis in our graphs. If this value of b
intersects the curve in the xb-plane
the intersection points correspond to the roots of the original equation for
that value of b. We have the following graph:
Graph B
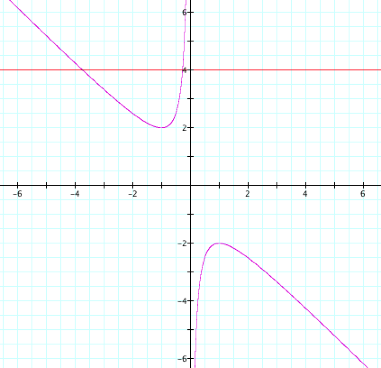
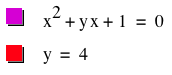
If we look at this graph, we
see that the red line, which represents b=4, intersects 
at two different points. What do these two intersections
represent? Since our graph is the
situation when b=4, then our
equation is 
. Algebraically,
if we solve for x using the quadratic formula, we get 
, or 
and 
. These two values are the roots of 
. Now, if we
look at Graph B to see how these
two x-values relate, it appears as
though these are the x-values
where the intersections of 
and 
occur. So does
this mean that that the intersection of 
with a value of b represents the real roots of the original
equation? LetŐs explore some more
values of b to see if this is
true!
If we look at Graph B, it looks as though the vertex of the top curve of the
hyperbola appears to be at b=2. By letting b=2, we get the following graph:
Graph C
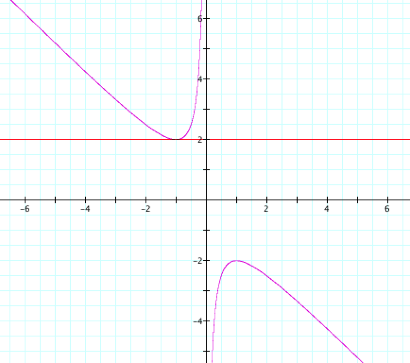
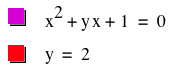
It appears that the line b=2 touches 
at one point. If we substitute b=2 into our equation to get 
and algebraically solve for x, we get 
, or 
. Once again,
is the root of 
and is also the x-value where the intersection of the two curves in Graph
C occurs.
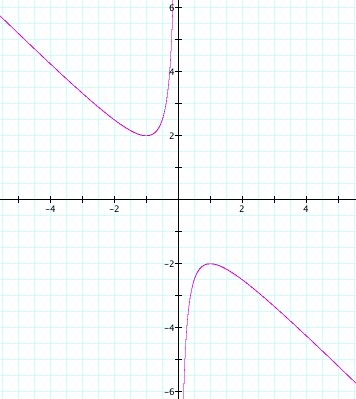
It is easy to see that if b=-4 and b=-2,
then similar results will be found because the bottom curve of the hyperbola
will be intersected by b=-4 in two
places and by b=-2 in two
places. But what about the area
between these two curves of the hyperbola? What would happen if we let b=-1?
LetŐs explore the graph of this situation!
Graph
D
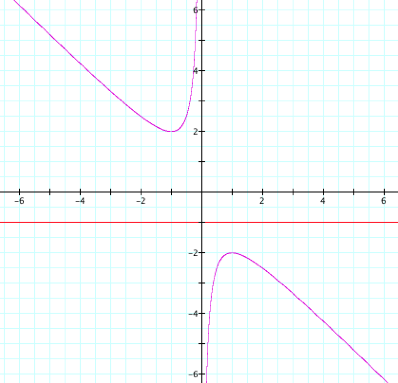
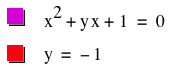
Clearly, 
does not intersect 
at any points. So what does this mean
algebraically? Using the quadratic
formula, we get 
, which has only non-real roots. Hence, when 
there are no real roots.
It appears that for each
value of b we select, we get a
horizontal line that either does or does not intersect our equation 
. From Graphs
A-D, it is clear that on a single
graph we get the following:
á
Two negative real roots
of the original equation when b
> 2
á
One negative real root
when b = 2
á
No real roots for -2
< b < 2
á
One positive real root
when b = -2
á
Two positive real roots
when b < -2
Consider the case when c = - 1 rather than + 1 in the equation 
. LetŐs
graph other values of c on the xb-axis and explore the graph! Click the picture below for a movie!
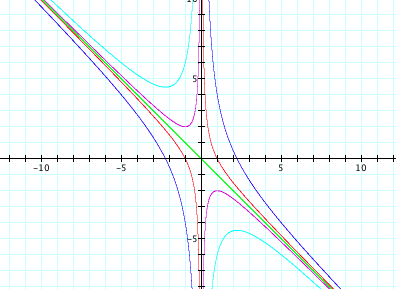
Graph E
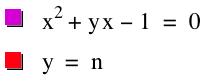
The moving red line in Graph
E represents all the different values
of b in the domain. If we look at the relationship between the
purple curve and the red line, we see that the red line always intersects the
purple curve in exactly two places.
Since in the previous graphs we discovered that the intersections
represented real roots of the quadratic equation, then we can check to see if
this is true. Using the quadratic
formula, we get 
, which will always have two real solutions since 
is always positive. Thus, when 
,
the equation 
always has two real roots for
all values of b.
Why is there a difference in
the number of solutions for when 
and 
? LetŐs graph 
for other values of c.
Graph F
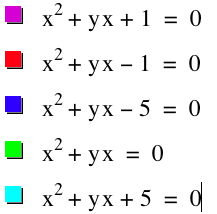
It appears that for each
value of c we select, we get a
hyperbola or a line. From Graph
F, it is clear that on a single graph
we get the following:
á
When 
, there
exists a b value such that there
are exactly two real roots, exactly one root, or no roots.
á
When 
, the
equation 
is a straight
line and there are always exactly two real roots for all values of b.
á
When 
, the
equation 
is a hyperbola
and there are always exactly two real roots for all values of b.