Parametric
Curves
By Courtney
Cody
In this assignment, we will investigate the following parametric equations:
for 
for different
values of a and b. Next, we will investigate the graphs
when the 
and 
components of the parametric equations are raised to a power,
such as
for 
and
for 
etc.
LetÕs begin by
graphing the general case when a = b = 1:
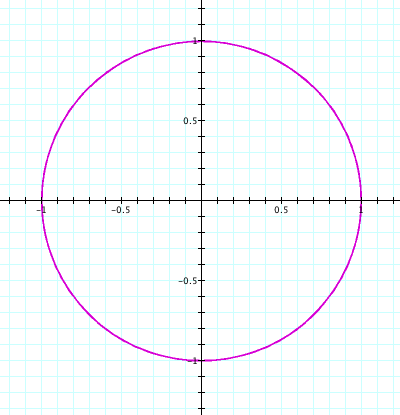
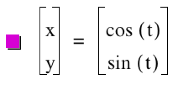
This is the graph
of a circle with a radius of 1. Hence,
the equations 
describe the
unit circle!
Now letÕs graph
the case where a=b (a and b are positive real numbers) for various
values on same coordinate plane:
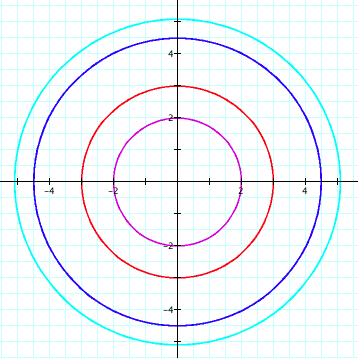
It is obvious that when a and b are positive real numbers and a=b, then 
are the
equations of a circle with a radius of a (=b)
What if we negate
the values of a and b in the previous example? How would this affect our graph?
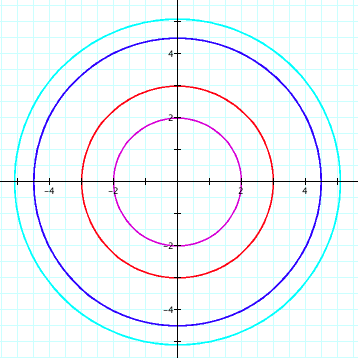
By looking at the
graph it appears as though nothing has changed. Is this true?
Even though the graph looks the same as when a and b are positive, we can no longer say that
the radius is a or b since a radius cannot be negative since it is a measure of
length. Thus, in the case where a and b are negative and a=b, the radius is the absolute value of a and b. Can we
generalize what the graphs of 
will look like
when a=b for all real
numbers a, b? Sure we can! When a=b the parametric equation is a circle
centered at the origin with a radius of 
.
What would the
parametric curves look like for the case when a<b for positive real numbers a
and b?
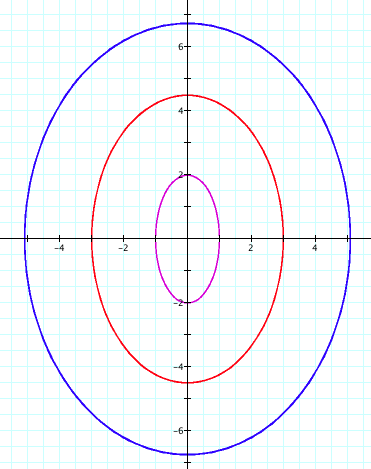
This graph
resembles the graph of the circle except stretched vertically. In particular, the graph is an ellipse centered
at the origin.
What if
a>b?
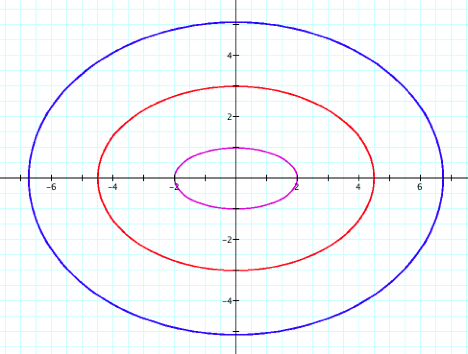
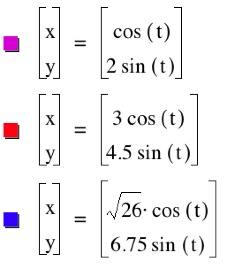
Again, it looks
like our circle has been stretched—horizontally this time—into an
ellipse.
Therefore, when
a and b are not equal the graph is an ellipse
centered about the origin. Notice
that when a=2 and b=1 the ellipse stretches from -2 to 2 on
the x-axis and from -1 to 1 on the y-axis. Similarly, when a=3 and b=2
the ellipse stretches from -3 to 3 on the x-axis and from -2 to 2 on the
y-axis.
In general, we
can say that when a<b
the equations 
form an ellipse
with a major axis of length 2b and a minor axis of length 2a.
When a>b,
the graph is an ellipse with a major axis of length 2a and a minor axis of length 2b.
Now we will
investigate the effect that increasing the powers of the 
and 
components of the parametric equations. LetÕs begin by graphing the first five
powers on the same coordinate place and weÕll let a=b=1.
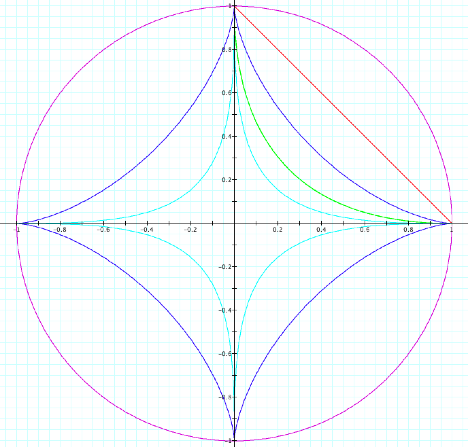
From the graph, we
can see that some of the parametric equations lie in all four quadrants while
some lie only in the first quadrant of the coordinate place. By looking at the equations and the
graph, we see a pattern that explains this observation. When the powers of the 
and 
components of the parametric equations are odd, the graphs of
the corresponding parametric equations lie in all four quadrants of the
coordinate plane. Also, when the
powers of the 
and 
components of the parametric equations are even, the graphs
of the corresponding parametric equations lie just the first quadrant of the
coordinate plane. We can also see
that the x- and y-intercepts are 
. Furthermore,
as the powers of 
and 
increase, the
graphs of the parametric equations curve more and more becoming closer to the
origin.
Next we will look
at the different parametric equations when 
, or 
and 
.
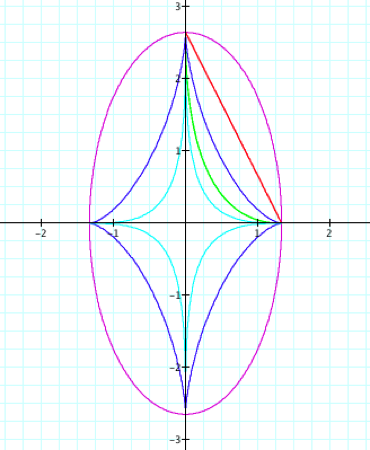
If we recall from
the beginning of this investigation, we found that the parametric equations 
when 
form an ellipse
with a major axis of 2b
and a minor axis of 2a. When we graph of the same plane the
parametric equations with increasing powers of the 
and 
components, we see that all of the graphs of the equations
where the power is greater than 1 fit inside of the ellipse. Additionally, the same observations as
in the previous example still hold.
We can also see that the x-intercepts are 
and the y-intercepts are 
.
Next we will look
at the different parametric equations when 
, or 
and 
.
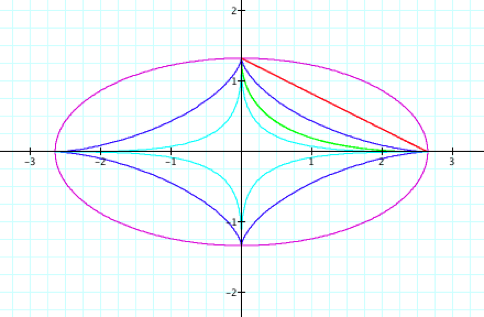
This graph is
very similar to the previous example except that the parametric equations 
when 
form an ellipse
with a major axis of 2a
and a minor axis of 2b and
the x-intercepts are 
and the y-intercepts are 
. All other
observations we have made thus far still hold.
Thus far, we have
only considered positive values of a and b. What if only one of a or b is negative.
WeÕll start by examining the example where 
and 
.
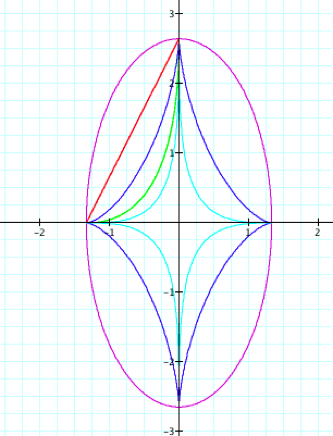
It is obvious
from looking at the graph that the only change we see is that the parametric equations
with even powers of 
and 
changed from
lying only in the first quadrant to lying only in the second quadrant. All other previous observations still
hold.
Now what if 
and 
?
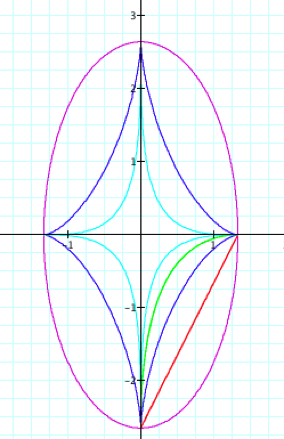
It is obvious
from looking at the graph that the only change we see yet again is that the
parametric equations with even powers of 
and 
changed to lying
only in the fourth quadrant. All other
previous observations still hold.
Now letÕs suppose
that both of a and b
are negative. Specifically, weÕll let 
and 
?
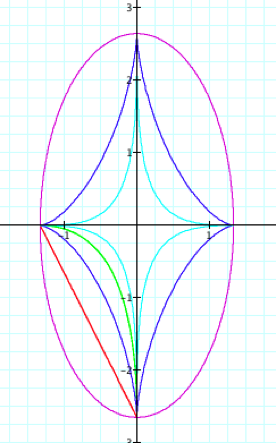
Once again, we
can see that the parametric equations with even powers of 
and 
changed to lying
only in the third quadrant this time and all other previous observations still
hold.
**********
In Conclusion,
for increasing powers of 
and 
in the parametric
equations 
á
The graphs
of the parametric equations with even powers of 
and 
lie in only one
quadrant while the graphs of the parametric equations with odd powers lie in
all four quadrants.
á
When 
and 
, the
graphs of the parametric equations with even powers of 
and 
lie in the first
quadrant.
á
When 
and 
, the
graphs of the parametric equations with even powers of 
and 
lie in the
second quadrant.
á
When 
and 
, the
graphs of the parametric equations with even powers of 
and 
lie in the third
quadrant.
á
When 
and 
, the
graphs of the parametric equations with even powers of 
and 
lie in the fourth
quadrant.