Polar
Equations
By Courtney
Cody
In this assignment, we will investigate the following polar equations for different
values of p:
for k > 1, k = 1, and k<1.
LetÕs begin by
considering just the first polar equation, 
, for different values of p and k.
First weÕll
consider the general case of this polar equation p = k = 1:
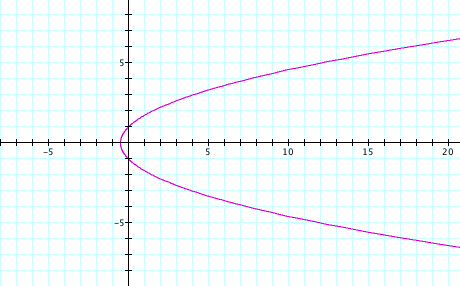
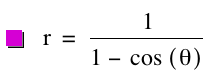
By studying the
graph, we first notice that our equation for r is not a function since it does not pass
the vertical line test. It does,
however, look like a sideways parabola opening up to the right. To confirm this observation, letÕs
observe the graph when k
= 1 and p = 4.
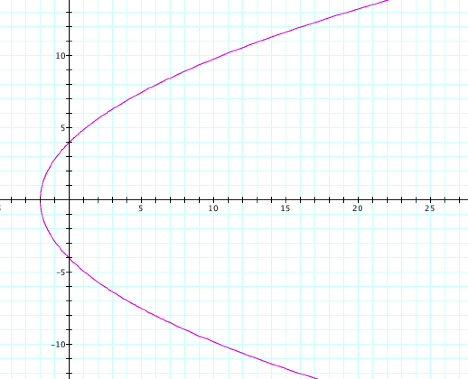
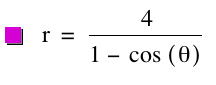
Once again, we
see that the graph when k = 1 and p
is varied is a parabola, only this second graph is wider. Hence it appears that p is a scalar and that the k = 1 causes the graph to be a
parabola. Thus, the equation, 
, where k = 1 and p
is varied is the polar equation of a parabola.
Next weÕll
consider the case of this same polar equation k < 1 and p is varied. Consider the following graphs for k = 0.5, p = 1; k = 0.5, p = 
; and k = 0.5, p
= -2, respectively.
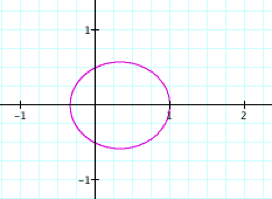
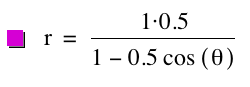
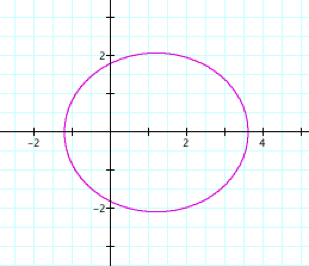
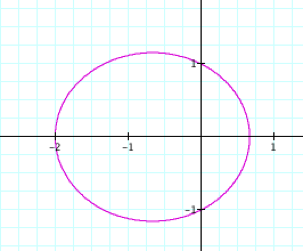
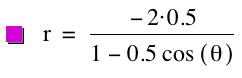
By observing the
graphs when k < 1
and p is varied we see
that it is an ellipse. Another aspect
of the graph that we can see is the furthest distance a point on the ellipse is
away from the origin is p units. Additionally
the y-intercepts are always 
.
Once again weÕll
consider this same polar equation but for the case when k > 1 and p is varied. Consider the following graphs for k = 1.1, p = 1; k = 1.1, p = 
; and k = 1.1, p
= -2, respectively.
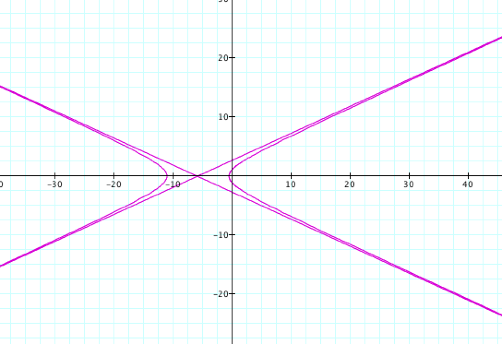
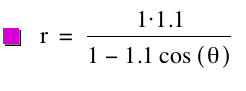
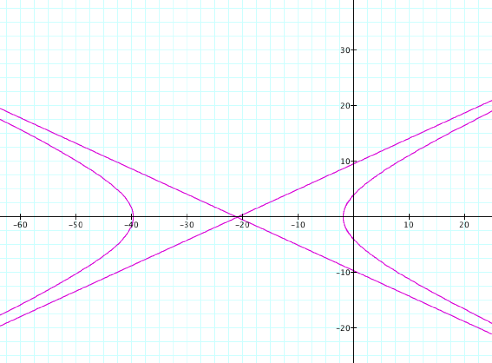
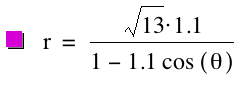
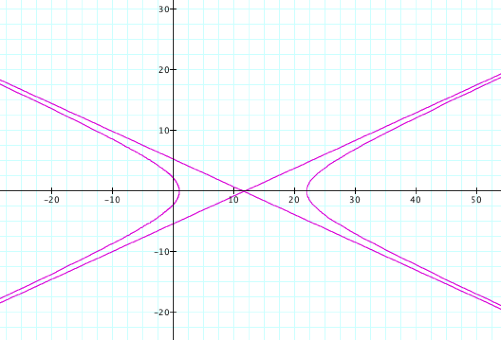
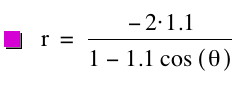
By observing the
graphs when k >1
and p is varied we see
that it is a hyperbola and its asymptotes.
Now we will
consider the second polar equation, 
, for different values of p and k.
First weÕll
consider the general case of this polar equation p = k = 1:
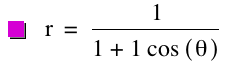
By studying the graph,
we notice that it looks like a sideways parabola opening up to the left. To confirm this observation, letÕs
observe the graph when k
= 1 and p = 4.
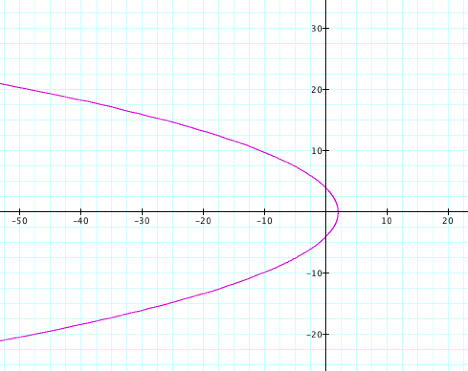
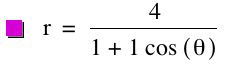
Once again, we
see that the graph when k = 1 and p
is varied is a parabola, only this second graph is wider. Hence it appears that p is a scalar and that the k = 1 causes the graph to be a
parabola. Thus, the equation, 
, where k = 1 and p
is varied is the polar equation of a parabola.
Next weÕll
consider the case when k
< 1 and p is varied
for the second polar equation.
Consider the following graphs for k = 0.5, p = 1; k =
0.5, p = 
; and k = 0.5, p
= -2, respectively.
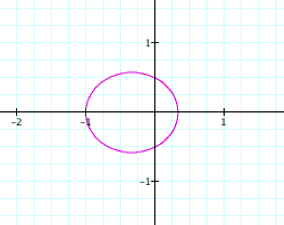
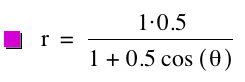
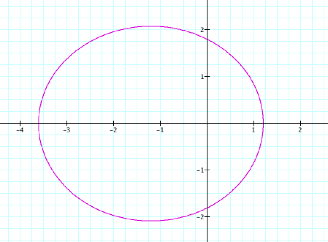
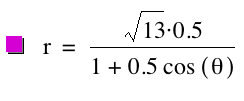
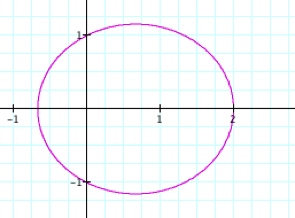
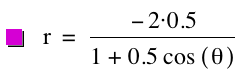
By observing the
graphs when k < 1
and p is varied we see
that it is an ellipse similar to the one for the first polar equation. In addition, we can see the furthest
distance a point on the ellipse is away from the origin is once again p units and the y-intercepts are always 
.
Seeing as how the
conic sections have been of the same type for the different polar equations
thus far, what do we expect for the case when k > 1 and p is varied? For the previous polar equation we graphed a hyperbola. To test our hypothesis, weÕll consider
the following graphs for k = 1.1, p
= 1; k = 1.1, p = 
; and k = 1.1, p
= -2, respectively.
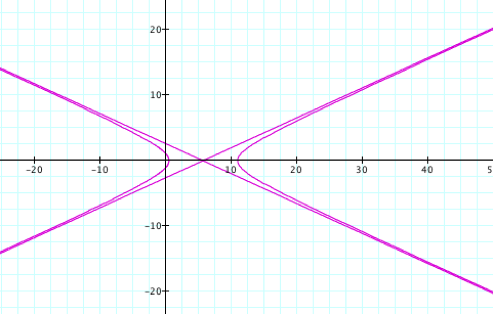
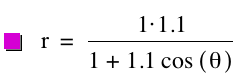
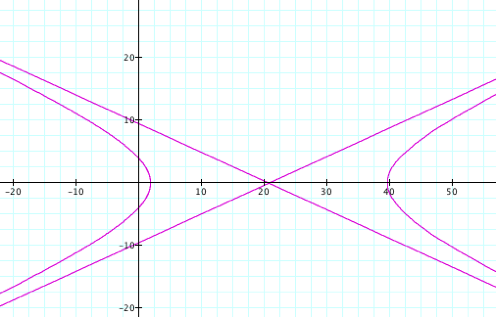
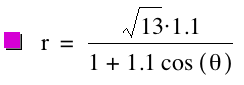
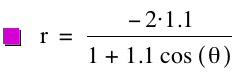
By observing the
graphs when k >1
and p is varied we see
that it is a hyperbola and its asymptotes, as we expected!
For the next two
polar equations, we will investigate the effect on the graphs from replacing 
with 
. We will begin
by considering the second polar equation, 
, for different values of p and k.
First weÕll
consider the general case of this polar equation p = k = 1:
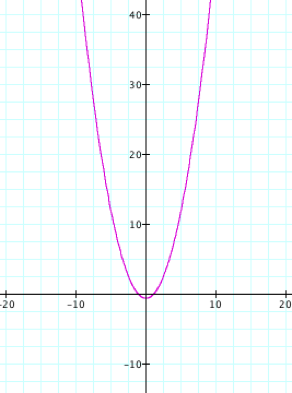
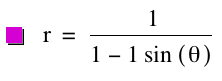
By studying the
graph, we notice that it looks like a parabola opening up. This is the same parabola as in the
first polar equation only rotated 180 degrees. To confirm this observation, letÕs observe the graph when k = 1 and p = 4.
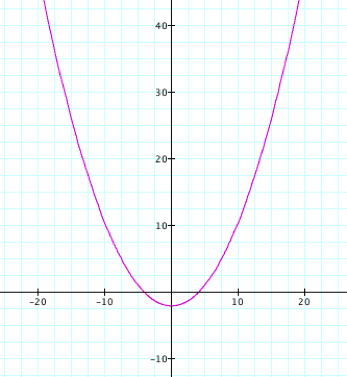
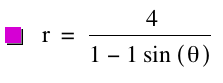
Once again, we
see that the graph when k = 1 and p
is varied is a parabola, only this second graph is wider. Hence it appears that p is a scalar and that the k = 1 causes the graph to be a
parabola. Thus, the equation, 
, where k = 1 and p
is varied is also a polar equation of a parabola.
Next weÕll
consider the case when k
< 1 and p is varied
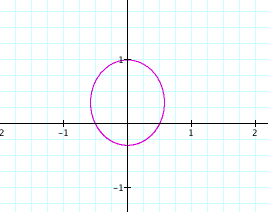
for the third polar equation. Consider
the following graphs for k = 0.5, p
= 1; k = 0.5, p = 
; and k = 0.5, p
= -2, respectively.
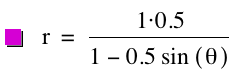
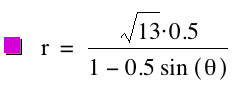
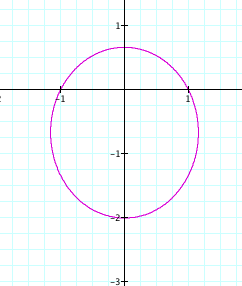
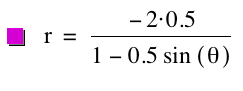
By observing the
graphs when k < 1
and p is varied we see
that it is an ellipse that is elongated vertically. In addition, we can see the furthest distance a point on the
ellipse is away from the origin is once again p units. In this case, the x-intercepts are always 
.
Seeing as how the
conic sections have been of the same type for the different polar equations
thus far, what do we expect for the case when k > 1 and p is varied? For the previous polar equations we graphed a hyperbola
opening to the left and right.
Since our ellipse rotated 180 degrees when we replaced 
with 
, we expect our hyperbola to rotate similarly. To test our hypothesis, weÕll consider
the following graphs for k = 1.1, p
= 1; k = 1.1, p = 
; and k = 1.1, p
= -2, respectively.
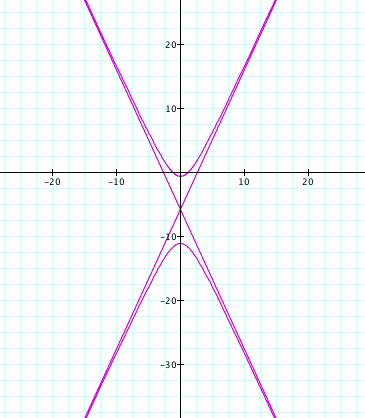
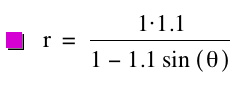
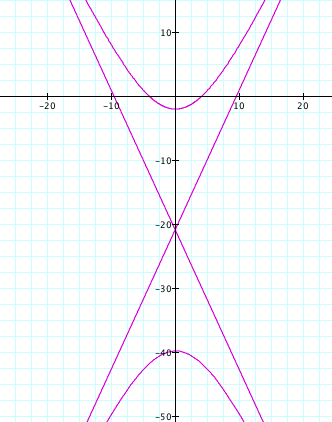
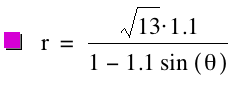
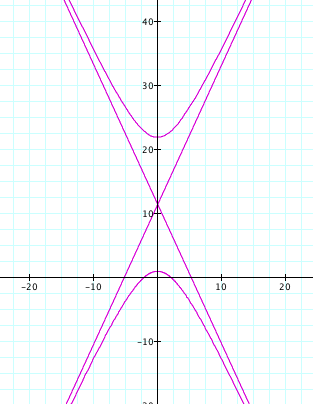
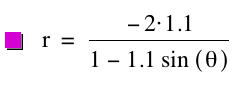
By observing the
graphs when k >1
and p is varied we see
that it is a hyperbola opening upward and downward and its asymptotes, as we
expected!
For the fourth
polar equation, we will consider the second polar equation, 
, for different values of p and k.
First weÕll
consider the general case of this polar equation p = k = 1:
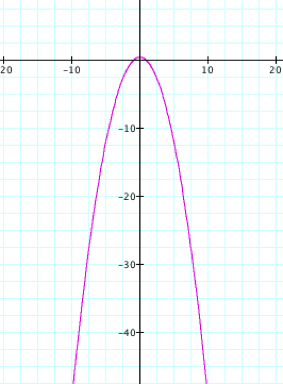
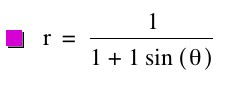
By studying the
graph, we notice that it looks like a parabola opening downward. This is the same parabola as in the
second polar equation only rotated 180 degrees. To confirm this observation, letÕs observe the graph when k = 1 and p = 4.
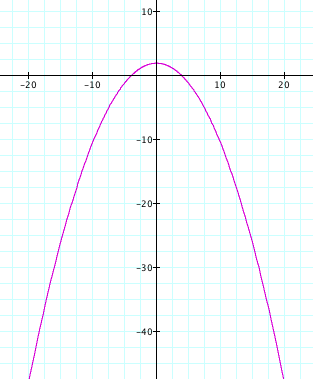
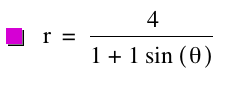
Once again, we
see that the graph when k = 1 and p
is varied is a parabola, only this second graph is wider. Hence it appears that p is a scalar and that the k = 1 causes the graph to be a
parabola. Thus, the equation, 
, where k = 1 and p
is varied is also the polar equation of a parabola opening downward.
Next weÕll
consider the case when k
< 1 and p is varied
for the fourth polar equation.
Consider the following graphs for k = 0.5, p = 1; k =
0.5, p = 
; and k = 0.5, p
= -2, respectively.
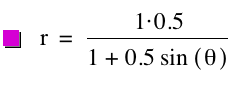
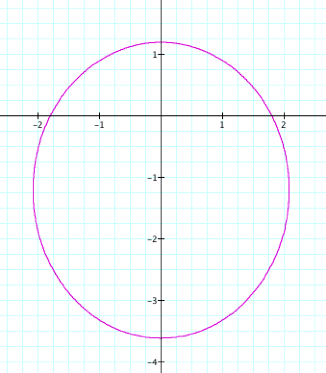
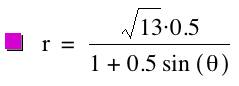
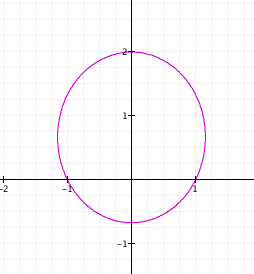
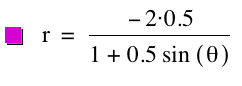
By observing the
graphs when k < 1
and p is varied we see
that it is an ellipse that is elongated vertically. In addition, we can see the furthest distance a point on the
ellipse is away from the origin is once again p units. In this case, the x-intercepts are always 
.
Using the
patterns we have observed for the different polar equations thus far, what do
we expect for the case when k > 1 and p is varied for the fourth polar equation? For the previous polar equations we
graphed a hyperbola opening to the left and right. Since our ellipse rotated 180 degrees when we replaced 
with 
, we expect our hyperbola to rotate similarly. To test our hypothesis, weÕll consider
the following graphs for k = 1.1, p
= 1; k = 1.1, p = 
; and k = 1.1, p
= -2, respectively.
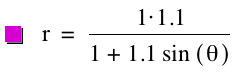
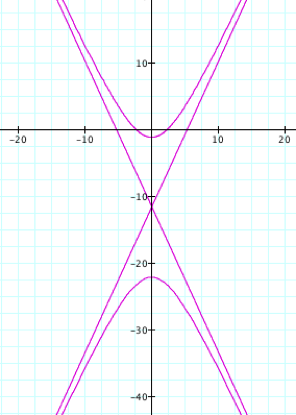
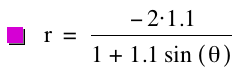
By observing the
graphs when k >1
and p is varied we see
that it is a hyperbola opening upward and downward and its asymptotes, as we
expected!