
Ellipses
and Hyperbolas
By Courtney
Cody
In this assignment, I will
construct the locus of points equidistant from a fixed point F and a
circle. Let F be any point in the plane
other than the center of the circle. Assume F is not on the circle; it can be
either inside or outside.
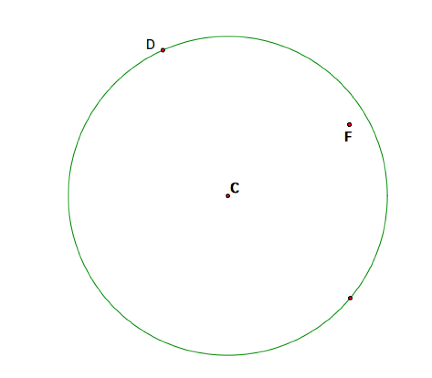
We’ll begin our construction
with an arbitrary circle and a point not on the circle. In particular, let the point not on the
circle be point F and let it lie inside the circle. In addition, let D be some point on the circle and the
center of the circle is point C.
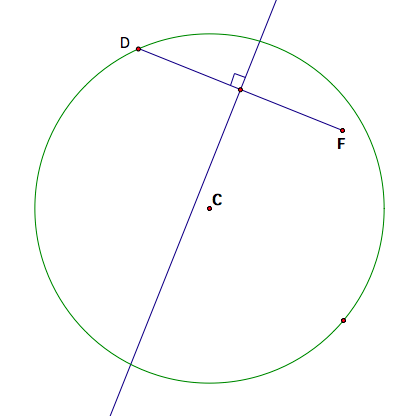
Since we want to construct
the locus of points equidistant from a fixed point F and a circle, we will
construct the segment between points D and F and find the midpoint of this
segment. Now, if we construct the
perpendicular bisector of this segment, this represents all points equidistant
from D and F.
If we recall from our
assumption, we let D be any point on the circle. Hence, the perpendicular bisector of the segment between
points D and F is specific to the location of D on the circle. So if we drag D around the circle, we
should expect numerous different perpendicular bisectors to form. Let’s take a look at the many lines
that result, which are pictured in red!

It appears as though all of
the different perpendicular bisectors of the segment between D and F for all D
on the circle trace an elliptical shape!!! More specifically, the intersection of the line through D
and C and the perpendicular bisector of segment DF is a point that traces an
elliptical shape. Even more, this
is the point where the perpendicular bisector is tangent to the ellipse!!!
By definition, an
ellipse is the set of
all points such that the sum of the distances from each foci to a given point
is constant.
Suppose we want to prove that our
construction is in fact an ellipse.
Let the point that traces the ellipse be point P and let the midpoint of
the segment between D and F (DF) be point M. Also, if we construct the segments PF and PM then we notice
that two triangles are form: triangle DMP (Purple) and triangle FMP (Yellow).
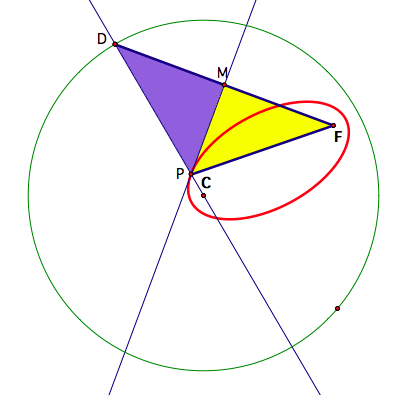
Since these triangles share a side
PM, then by the reflexive property, PM is congruent to PM. Also, since
the tangent line from the construction is the perpendicular bisector of segment
DF, then angles DMP and FMP are both 90 degrees and are congruent. This perpendicular bisector also
implies that DM is congruent to FM.
Hence, by the side-angle-side congruence axiom the two triangles are
congruent.
By the definition of ellipse, we need to show that the sum of the distances from a
point on the ellipse to the two foci is a constant. Since the two triangles are congruent, then segment PD is
congruent to FP. Since P also lies
on segment CP, then CP + PD = CD.
If we combine the equations together then the sum CP + FP is equal to
CD, which is the radius of the circle and a constant, as desired.
Thus, our construction is in fact an
ellipse and points C and F are the two foci of the ellipse.
Well… what if our original
construction was based on point F lying outside of the circle. How would this change our
construction? Using the same exact
procedure to construct the locus of points when F lies outside of the circle,
we obtain the following:

At the instant point F
crossed to the outside of the circle, the locus of points changed from and
elliptical shape to a hyperbolical shape!
By definition, a hyperbola is the set of all points such that the difference
of the distances from each foci to a given point is constant.
Suppose we want to prove that
our new construction when point F is outside of the circle is a hyperbola. Similar to the proof of the ellipse, we
have the following diagram:
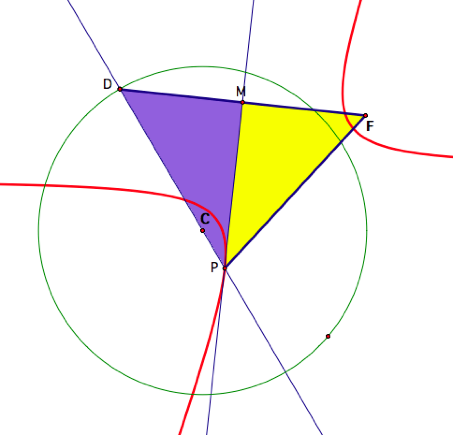
Since the purple and yellow
triangles share a side PM, then by the reflexive property, PM is congruent to
PM. Also, since the tangent line from the construction is the
perpendicular bisector of segment DF, then angles DMP and FMP are both 90
degrees and are congruent. This
perpendicular bisector also implies that DM is congruent to FM. Hence, by the side-angle-side congruence
axiom the two triangles are congruent.
By the definition of hyperbola, we need to show that the difference of the distances
from each foci to a given point is constant. Since the two triangles are congruent, then segment PD is
congruent to FP. Since P also lies
on segment CP, then PD - CP = CD.
If we combine the equations together then the sum FP - CP is equal to
CD, which is the radius of the circle and a constant, as desired.
Thus, our construction when
point F lies outside of the circle is in fact a hyperbola and points C and F
are the two foci of the hyperbola.