
Tangent
Circles
By Courtney
Cody
In this assignment, I will investigate tangent circles. I will begin by constructing one instance of tangent circles
before showing the locus of the center of the constructed circle is either an
ellipse or a hyperbola depending on the position of the two given circles.
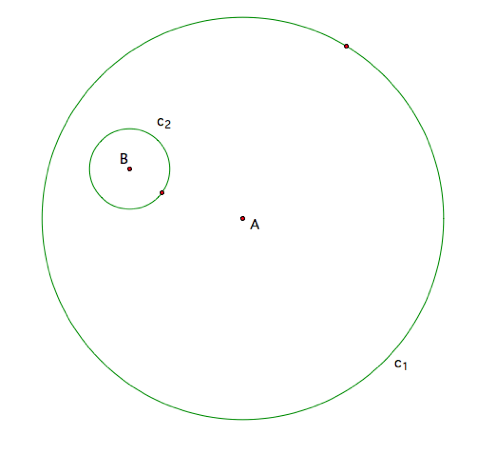
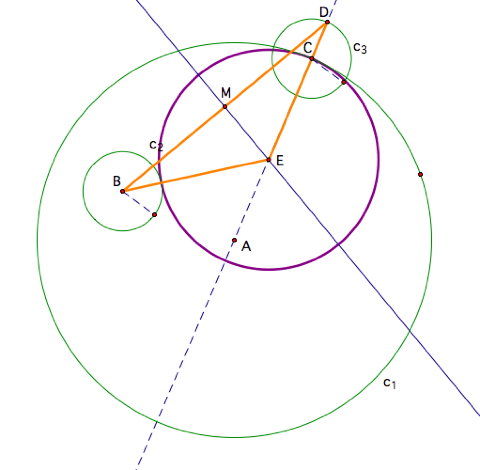
We begin our
construction with two arbitrary circles where the smaller circle c2
with radius A lies within, but not touching the larger circle c1
with radius A.
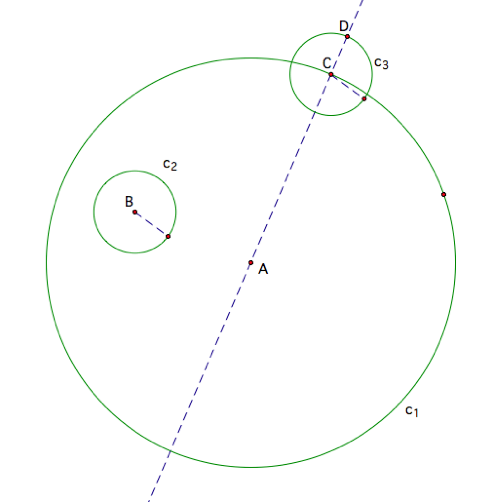
Now, suppose we have a point
C that lies at some point on the larger circle. LetŐs construct the line through C and center A. Also, we want to create a new circle c3
with the same radius of the smaller circle and center C of the outside
circle. Next, let the point where
this third circle intersects the line through points C and A be called point D.
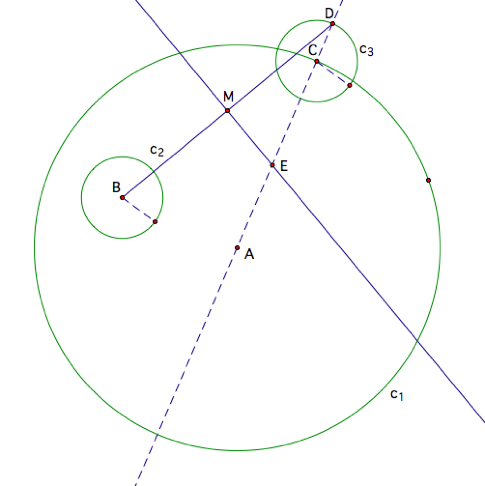
We will now construct the
line segment from B to D, find the midpoint (M) of this segment, and then
construct the perpendicular bisector of the segment using GSP
capabilities. The point where the
perpendicular bisector hits the line that is inside the circle we will label E.
We can also now construct an
isosceles triangle BED, which is pictured in orange.
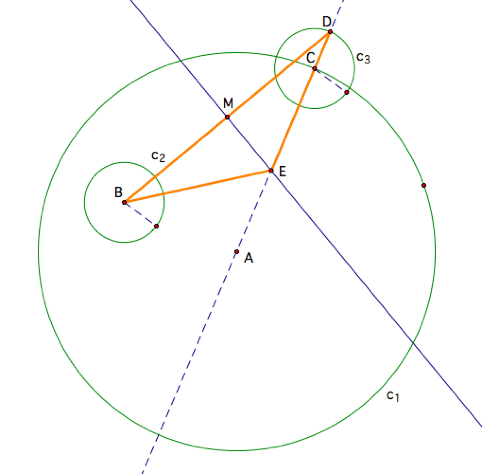
Lastly, we can construct our desired
tangent circle whose center is the vertex of the isosceles triangle and the
radius being the distance from point E to the center of the third circle c3. Hence, the isosceles triangle is what
allowed us to see how to construct the tangent circle since the length of each
leg is the sum of the radii of the small circle and the tangent circle. This tangent circle is pictured in purple.
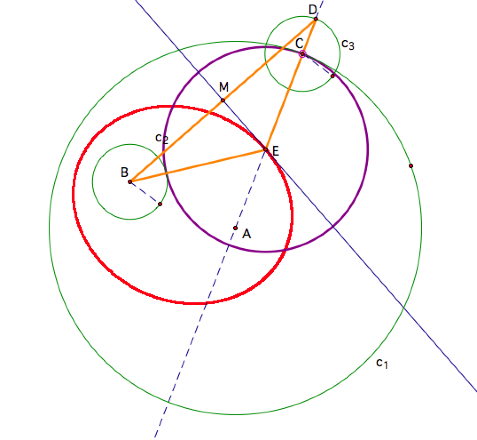
If we animate the point on
circle c1 (point C) and trace the center of the tangent circle
(point E), then point E traces a new, non-circular curve. It appears that the
locus of the center of the tangent circle is an ellipse where the centers of
the two given circles (c1 and c2) are the foci. See the red
locus of points below.
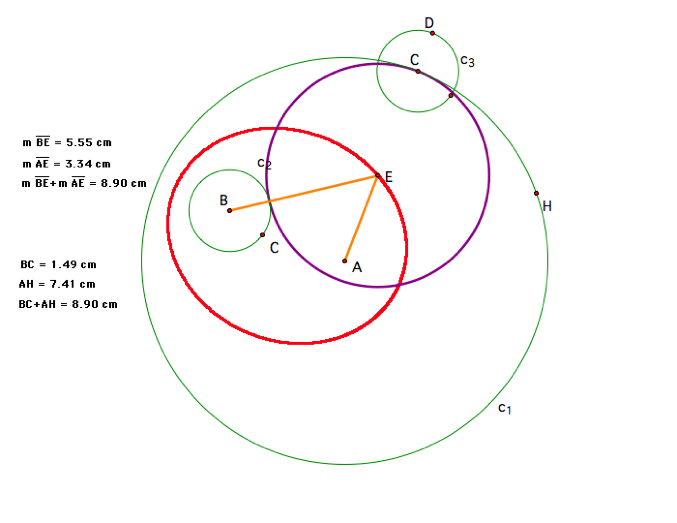
To see why the locus of
points is an ellipse, letŐs construct segments from each of the two foci
(points A and B) to the center of the tangent circle (point E). Using the measurement tool in GSP, we
see that the sum of the two segments is equal the sum of the radii of the two
given circles, which is always constant. Thus, by definition, the locus of
points is an ellipse with the centers of the two given circles as the
foci.
Now, suppose the two given
circles intersected. LetŐs see
what the locus of points would look like for this case.
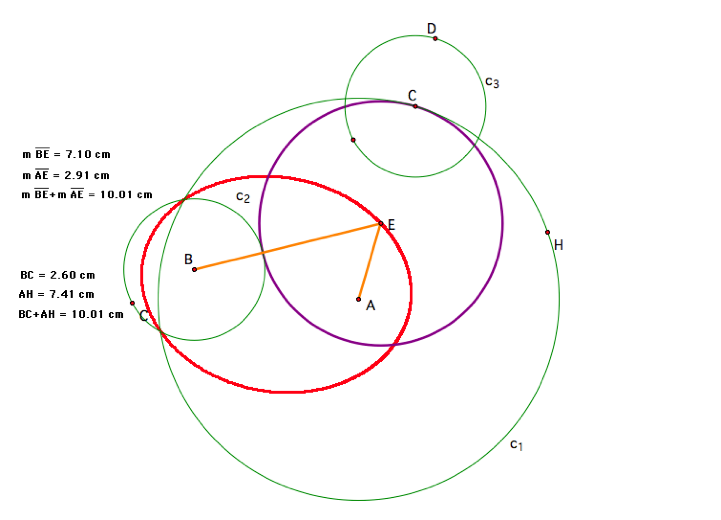
Keeping everything in the
construction the same except moving circle c2 such that it
intersects circle c1, we see that the locus of the center of the
tangent circle is still an ellipse with focal points A and B. Additionally, if we look at the measurements
to the left of the diagram above, we see that the sum of the lengths of the
segments drawn from the foci to the center of the tangent circle is again equal
to the sum of the radii of the two given circles. Thus, by definition, the locus of points is again an
ellipse.
Now, suppose the two given
circles intersected. LetŐs see
what the locus of points would look like for this case.
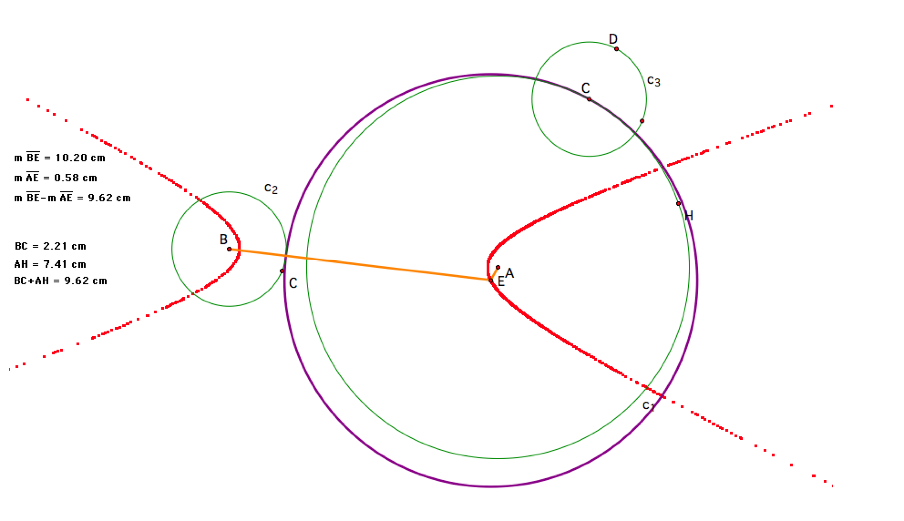
The locus of points appears
to be a hyperbola. Hence, in the
case where circles c1 and c2 are disjoint, the difference,
not the sum, of the segments from
each of the two foci (points A and B) to the center of the tangent circle
(point E) is equal to the sum of the radii of circles c1 and c2,
which is always constant.
Additionally, if we look at the measurements to the left of the diagram
above, we see that the difference of the lengths of the segments drawn from the
foci to the center of the tangent circle is equal to the sum of the radii of
the two given circles. Thus, the locus
of points is a hyperbola and points A and B are the foci of the hyperbola.
Click here
to play around with the tangent circles yourself!