
Orthocenter
and Altitude Ratios
By Courtney
Cody
In this assignment, I will investigate the altitude ratios created by a triangleŐs
orthocenter. Specifically, given
triangle ABC, I will construct the orthocenter H, let points D, E, and F be the
feet of the perpendiculars from A, B, and C respectfully, and prove the
following equations:
![]()
![]()
Consider the following
triangle ABC:
Now, letŐs
construct the altitude for all three vertices and let points D, E, and F be the
feet of the perpendiculars from A, B, and C respectfully. We will mark the intersection of these
altitudes as point H. Recall that
a triangleŐs orthocenter is the intersection of these three altitudes. Hence, we have the following triangle
with orthocenter H:
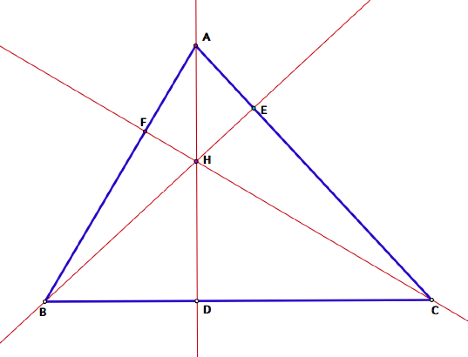
In order to help
with our proof, we will divide triangle ABC into three smaller triangles,
namely ACH, ABH, and ACH. These
are pictured below in orange, purple,
and green, respectively.
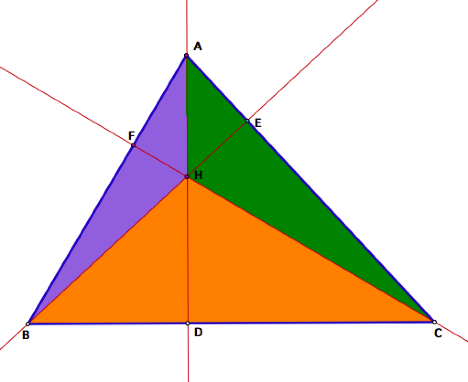
Since we know
these three smaller triangles make up the larger triangle ABC, we have the
following equation:
![]()
Dividing the
entire equation by ![]() , we have:
, we have:
![]()
or
![]()
Since the
altitudes meet the sides of triangle ABC at right angles, then we can determine
the areas of all triangles in the diagram. Also, we can express the area of triangle ABC in three
different ways since there are three different altitudes and corresponding
sides, which we will carefully use since we are trying to form a particular sum
of ratios. Consider the following:
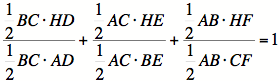
which reduces to
![]()
Thus, we have
established the first equation.
In order to prove
the second equation, we will begin with the first equation and make necessary
modifications. To begin, we will use
the drawing to express the segments represented by the numerators of each
proportion in the first equation as the difference of two other segments as
follows:
![]()
![]()
![]()
Substituting
these new representations into the first ratio, we have the following equation:
![]()
![]()
![]()
![]()
![]()
![]()
Thus, we have established
the second equation.
Recall that our
proofs of two equations were based on a given acute triangle. What if ABC is an obtuse triangle? Will our equations still hold? LetŐs think about this! If we drag point C such that angle CAB
is obtuse (greater than 90 degrees), then we notice that the orthocenter H
moves outside of triangle ABC. See
the diagram below:
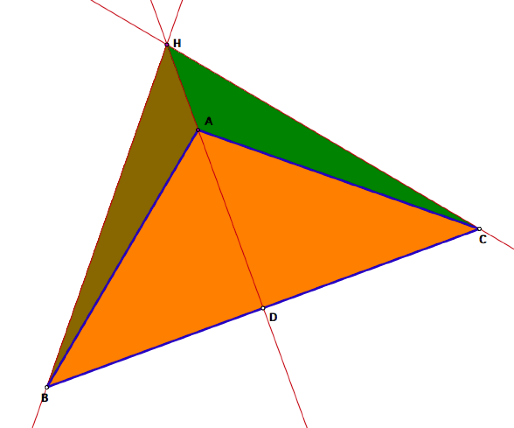
If the triangle
is obtuse, then it is obvious that points E and F disappear from the diagram since
their corresponding altitudes do not intersect the sides of triangle ABC. Hence, segments BE and CF are no longer
relevant, which means that the two equations proved in this exploration do not
apply to this diagram. Thus, the
two equations we proved do not hold when triangle ABC is obtuse.