Pedal
Triangles
By Courtney
Cody
In this assignment, we will
construct a pedal triangle where the pedal point P is any point in the
plane. Then we will explore the
case when P is the pedal point P is the centroid, circumcenter, incenter,
orthocenter, and center of the nine-point circle of a given triangle.
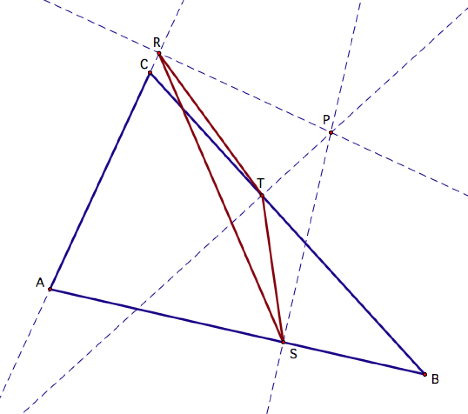
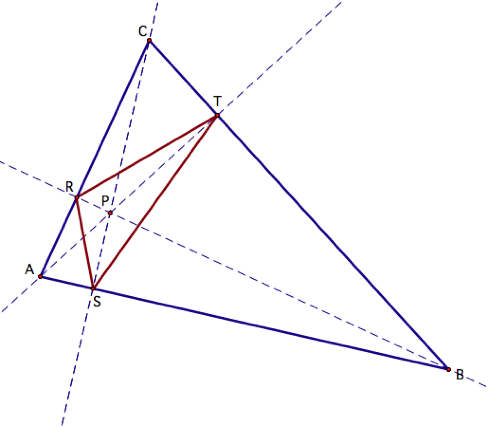
Suppose we have an arbitrary
triangle ABC and let P be any point on the plane. By constructing the perpendicular lines from each side of
triangle ABC to point P and calling the intersections of these lines points R,
S, and T, we have constructed a pedal triangle. Namely, the triangle formed by points R, S, and T is the
pedal triangle and P is the pedal point.
In this case, we have P lying outside of triangle ABC.
Click on the diagram above to
move vertices of triangle ABC and the pedal point P and observe how the pedal
triangle RST changes as these points are moved.
Now we will look at the cases
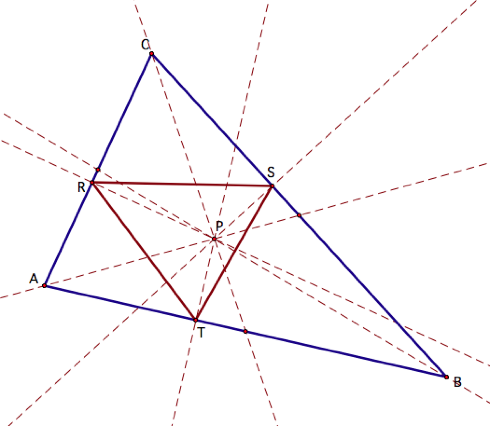
when the pedal point P is the centroid of triangle ABC. By definition, the centroid is the
common intersection of the three medians.
By constructing the centroid of triangle ABC and letting it be the pedal
point P, we can construct the pedal triangle about P.
If we study the diagram
above, we see that when the pedal point P is the centroid of triangle ABC, the
pedal triangle RST is always inside triangle ABC since the centroid is always
inside triangle ABC. Click on the
diagram above to move vertices of triangle ABC and the pedal point P and
observe how the pedal triangle RST changes as these points are moved when P is
the centroid.
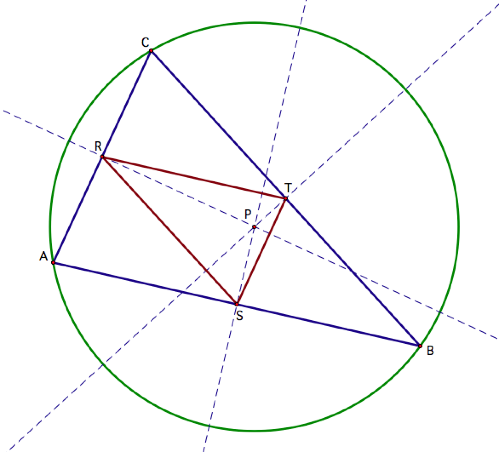
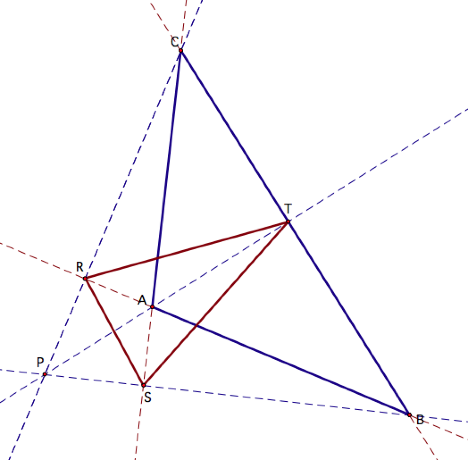
Now we will look at the cases
when the pedal point P is the circumcenter of triangle ABC. By definition, the circumcenter is the
intersection of a triangleÕs three perpendicular bisectors. By constructing the
circumcenter of triangle ABC and letting it be the pedal point P, we can
construct the pedal triangle about P.
If we study the diagram
above, we see that when the pedal point P is the circumcenter of triangle ABC,
and that the pedal triangle RST is actually the medial triangle since itÕs
vertices are the midpoints of the segments that make up triangle ABC. Additionally, since P is the center of
the circle that circumscribes triangle ABC then P is equidistant from all three
vertices. This implies that the
distance from P to each of the vertices A, B, and C is the radius of the
circles that circumscribes triangle ABC.
Click on the diagram above to move vertices of triangle ABC and the
pedal point P and observe how the pedal triangle RST changes as these points
are moved when P is the circumcenter.
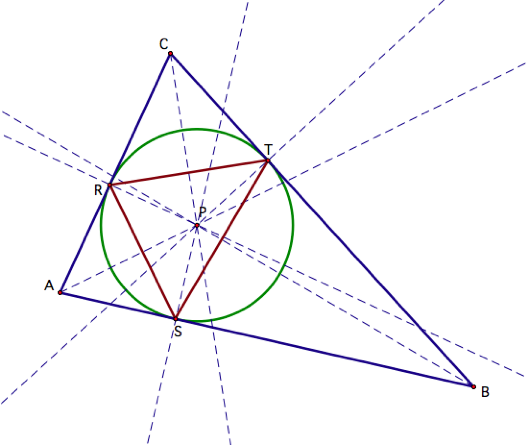
Now we will look at the cases
when the pedal point P is the incenter of triangle ABC. By definition, the incenter is the
common intersection of the three angle bisectors. By constructing the incenter of triangle ABC and letting it
be the pedal point P, we can construct the pedal triangle about P.
If we study the diagram
above, we see that when the pedal point P is the incenter of triangle ABC,
pedal triangle RST will also always be inside triangle ABC since the pedal
point P is the center of the circle that is inscribed in triangle ABC. Hence, P is always inside triangle
ABC. Additionally, since P is the
center of the circle that is inscribed by triangle ABC then P is equidistant
from all three vertices of the pedal triangle RST. This implies that the
distance from P to each of the vertices R, S, and T is the radius of the
circles inscribed by triangle ABC.
Click on the diagram above to move vertices of triangle ABC and the
pedal point P and observe how the pedal triangle RST changes as these points
are moved when P is the incenter.
Now we will look at the cases
when the pedal point P is the orthocenter of triangle ABC. In particular, weÕll start by looking
at an acute triangle ABC. By definition, the orthocenter is the
intersection of the three altitudes of a triangle. By constructing the orthocenter of acute triangle ABC and
letting it be the pedal point P, we can construct the pedal triangle about P as
pictured below:
When the pedal point P is the
orthocenter of triangle ABC, pedal triangle RST is also the orthic triangle,
which is defined as the triangle joining the feet of the altitudes of a
triangle. Since altitudes always
meet the sides of the larger triangle (ABC in this case), then this is how we
found the pedal triangle since it the vertices of RST are where the lines
perpendicular to the sides of ABC pass through P. Additionally, the pedal triangle is located entirely within
triangle ABC. Click on the diagram
above to move vertices of triangle ABC and the pedal point P and observe how
the pedal triangle RST changes when P is the orthocenter of an acute triangle.
What would happen if triangle
ABC were obtuse?
If triangle ABC were obtuse,
then we must extend the sides of the triangle in order to determine where the
altitudes intersect the sides of the triangle. Once we have constructed our pedal triangle RST, we notice
that it is located partially inside triangle ABC and partially outside. Also, our pedal point P is located
outside of triangle ABC. Hence,
the pedal point is called the exterior orthocenter. Click
on the diagram above to move vertices of triangle ABC and the pedal point P and
observe how the pedal triangle RST changes when P is the exterior
orthocenter.
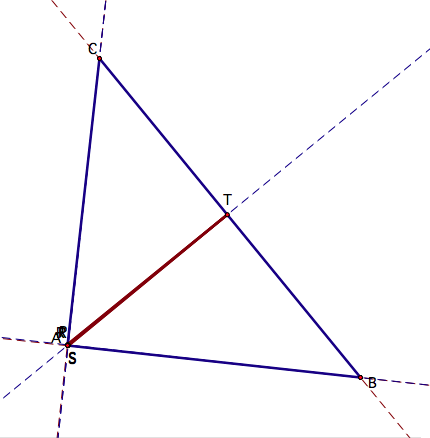
What about if triangle ABC
were a right triangle?
If
triangle ABC were a right triangle, then we notice that points A, P, R, and S
all converge. This is because when
we construct the altitudes of each vertex in order to find the orthocenter, two
of the altitudes lie directly on the two sides adjacent to the right
angle. The third altitude actually
bisects triangle ABC. Hence, the
orthocenter of a right triangle is located at the vertex of triangle ABC. Specifically, P is the vertex of the
right angle. Now, if we construct
the pedal triangle, since points P, R, and S lie on the same point, then the
only segment drawn for the pedal triangle is segment PT, which is the line that
bisects triangle ABC. Thus, the
pedal triangle is a line on an altitude of triangle ABC. Click on the diagram above to move
vertices of triangle ABC and the pedal point P and observe how the pedal
triangle RST changes when P is the orthocenter of right triangle ABC.