Bouncing
Barney
By Courtney
Cody
In this assignment, we will
investigate the situation of Bouncing Barney, who is in a triangular room
ABC. He walks from a point on BC
parallel to AC. When he reaches
AB, he turns and walks parallel to BC.
When he reaches AC, he turns and walks parallel to AB. We will explore and discuss BarneyŐs movement
for various starting points and we will prove that Barney will eventually
return to his starting point, including how many times will Barney reach a wall
before returning to his starting point.
LetŐs begin by sketching a
general diagram of BarneyŐs movement for some arbitrary starting point D on BC.
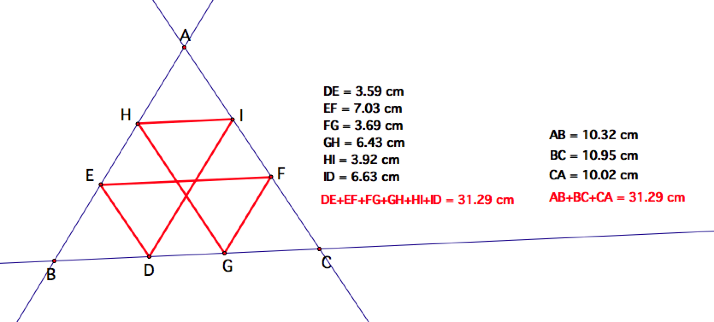
By studying the figure above,
BarneyŐs path was D-E-F-G-H-I-D and we see that every 3 steps Barney hits each
wall of the triangular room. Also,
it appears as though Barney will return to the starting point, for which he
traveled six paths in the diagram above.
Now let's explore BarneyŐs path
for a different starting point.
LetŐs have him start where D is the midpoint of segment BC.
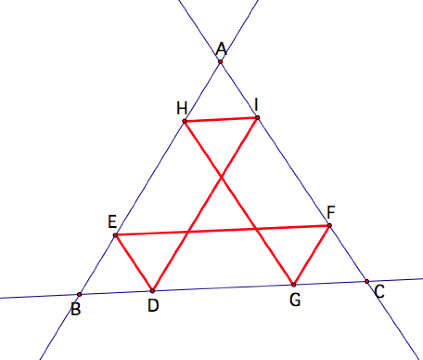
By studying this figure, we
see that when D is the midpoint of BC, then BarneyŐs path is the medial
triangle of the room. While the diagram shows us that he
returns to his starting point again, this time it appears as though it only
takes him three paths to get back to his starting point. While it is not immediately obvious,
upon closer investigation of the figure it appears as though the length of BarneyŐs
complete path is twice the length perimeter of the medial triangle and that
Barney returns to his starting point twice.
Now letŐs have Barney start
where D is one-third the length of segment BC.
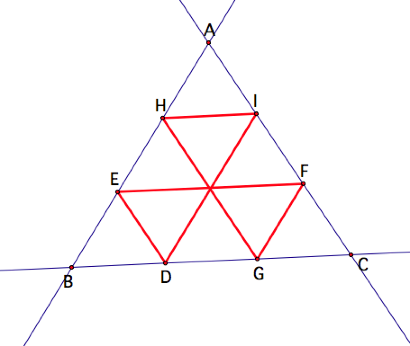
By having Barney start
one-third along BC we see that his path trisects each side of the triangular
room.
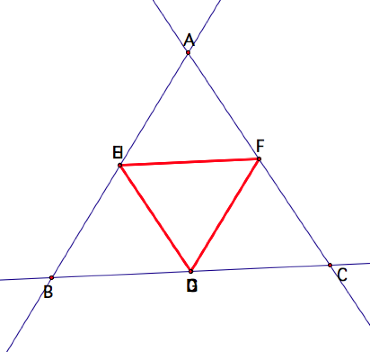
Now suppose Barney starts at
one of the vertices of the triangle, namely B. BarneyŐs path is as follows:
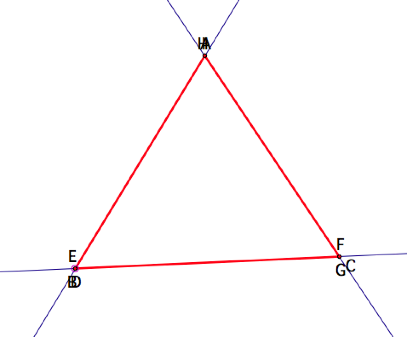
From the figure, we see that Barney
once again returns to his starting point and that it takes him three paths to
do so. In addition, BarneyŐs path
is the same as the length of the perimeter of the triangular room ABC.
Click HERE
to explore further BarneyŐs path for any starting point on BC!
Now that we have explored
BarneyŐs path for various starting points, it is significant to determine
whether the length of the path Barney has traveled is always constant. Click on the figure below for a GSP
construction to move BarneyŐs starting point D around to verify with
measurements that the length of his path is constant no matter where his
starting point is on BC.
PROOF
Now letŐs prove that Barney
will return to his starting point.
Suppose D is BarneyŐs
starting point and J is his ending
point.
As stated in the problem for
Bouncing Barney, DE is parallel to
AC. Then by the Angle-Angle similarity axiom we know that,
triangle BED is similar to
triangle BAC. Therefore, we can set up the proportion
.
Similarly, since EF is parallel to BC as stated in the problem, then we know that triangle AEF is similar to triangle ABC. Hence,
we can set up the proportion 
. Using these
first two proportions, we know that 
.
In keeping with this pattern
of similar triangles, we set up the following proportions:
This implies that 
, or 
.
Since we are trying to prove that
the next point J is equal to D in order to verify that the ending point is the
same as the starting point, we can set up another proportion to get 
since BarneyŐs
next direction must head parallel to AB and intersect BC and we are letting
this end point be J. Therefore, 
and so BarneyŐs
path will always begin and end at the same point and thus it is a closed
circuit, as desired.
How does BarneyŐs path change
if his starting point is outside of triangle ABC? Is the length of BarneyŐs path preserved when he starts
outside of the triangle? LetŐs
investigate!
If Barney starts on a point
not on a point on the line through AC but not on the segment AC and moves
parallel to BC, he must go towards AB if he wishes to change his direction
again. If he does this, he will see six different point, as in the usual case.
The proof of this fact is similar to the proof above.
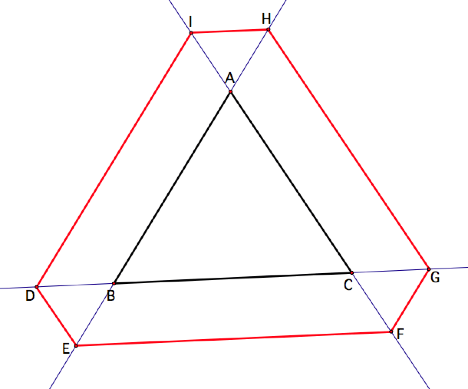
To see if length is preserved
when the starting point is outside of triangle ABC, letŐs make some
measurements. First, letŐs recall
how when D is inside of triangle ABC, BarneyŐs path is always the length of the
perimeter of triangle ABC. Now,
letŐs compare this fact to the case when D lies outside of ABC.
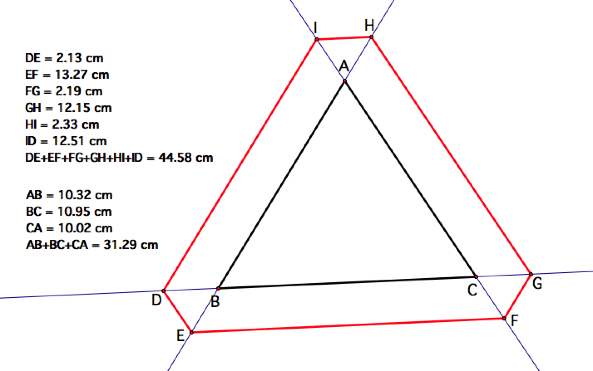
AND
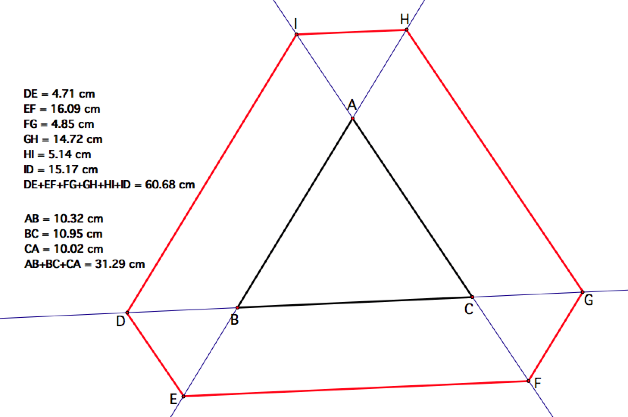
As we can see by comparing
the two diagrams above, the length of BarneyŐs path changes depending on how
far outside of triangle ABC he starts at (point D). Therefore, the length Barney travels is not preserved when
he starts outside of the triangle.
Click HERE
to see the effect of changing BarneyŐs starting point.