CevaÕs
Theorem
By Courtney
Cody
In this assignment, we will
investigate, prove, and extend CevaÕs Theorem.
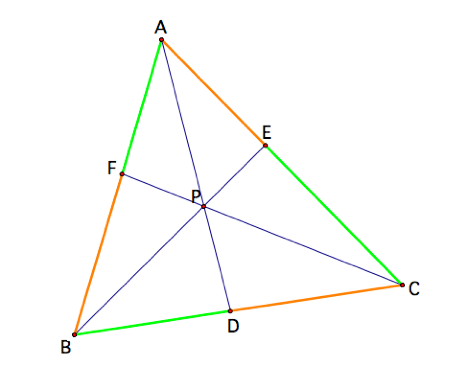
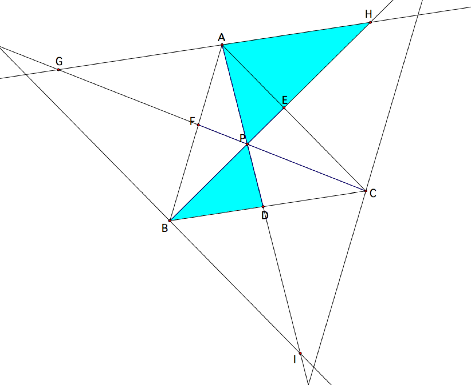
LetÕs begin by constructing a
diagram to represent CevaÕs Theorem.
Consider any triangle ABC.
Select a point P inside the triangle and draw lines AP, BP, and CP
extended to their intersections with the opposite sides in points D, E, and F
respectively. We wish to explore
the relationship between the products 
and 
, or the product of the left-hand-sides (green) and the
right-hand sides (orange) of each side of triangle ABC.
To begin our investigation,
we will the built-in measure and calculation tools to explore the relationship
between the two products.
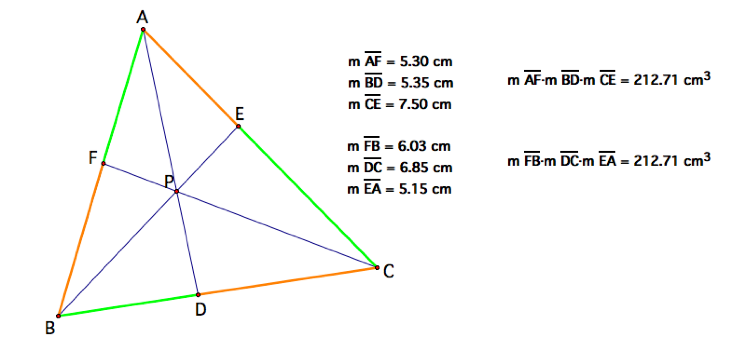
As we can see in the diagram
above, the products 
and 
appear to be
equal. Click HERE
to move the points of the triangle around to see if the products remain the
same.
THEOREM
CevaÕs theorem states that if points D, E, and F are on the sides AB, BC and AC of a triangle ABC then the lines AE, BF and CD are concurrent if and only if the
product of the ratios
.
PROOF
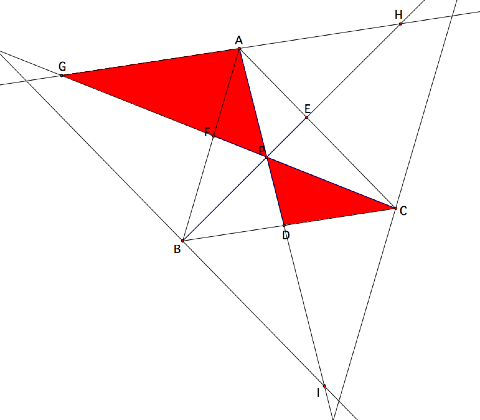
We will begin by assuming the
following diagram for some point P
inside the triangle:
Suppose we create a line
parallel to BC through A and extend the segments CF and BE
beyond the triangle to form points G
and H respectively as the lines
intersect the parallel line through A. Several sets of similar triangles form,
four of which we will pay particular attention to, which are described below.
(1) Triangle AFG is
similar to triangle CBF.
The two green triangles
pictured in the diagram above are similar because opposite angles 
AFG and 
BFC are
congruent, 
AGF and 
FCB are
alternate interior angles, and thus 
GAF and 
FBC are
congruent angles because all other corresponding angles are congruent and by
the triangle sum theorem the third corresponding angles in each of the two
triangles must be congruent.
Therefore, triangle AFG is
similar to triangle CBF.
Since AFG~BFC, we can set up the following proportion:
(2) Triangle BDP is
similar to triangle HAP.
By a similar method as in
(1), triangle BDP is similar to
triangle HAP. Since BDP~HAP, we can set up the following proportion:
(3) Triangle AHE is
similar to triangle CBE.
By a similar method as in
(1), triangle AHE is similar to
triangle CBE. Since AHE~CBE, we can set up the following proportion:
(4) Triangle APG is
similar to triangle DPC.
By a similar method as in
(1), triangle APG is similar to
triangle DPC. Since APG~DPC, we can set up the following proportion:
Hence, after exploring the
different similar triangles, we have the following four proportions:
(a) 
(b)
(c) 
(d) 
Since the ratio 
is common to
both (b) and (d), then we know that 
.
Since G is not a part of the original triangle, we want to
eliminate AG from the above
proportion. Hence, we can use (a)
to solve for AG and substitute.
Since 
, then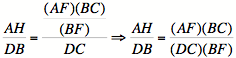 
.
Similarly, since H is not a part of the original triangle, we want to
eliminate AH from the above
proportion. Hence, we can use (c)
to solve for AH and substitute.
Since 
, then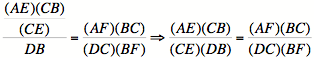 
.
Now, by the reflexive
property CB=BC, DC=CD, DB=BD, and
BF=FB.
Hence, making these
substitutions and rearranging the terms, we have
Thus, 
.
PROOF OF THE CONVERSE OF
CEVAÕS THEOREM
Consider any triangle ABC and let D, E, and F lie on segments BC,
AC, and AB respectively, all of which satisfy
.
Let P be the intersection
inside triangle ABC of the
segments CF and BE. Also,
let DÕ be the intersection of AP and BC.
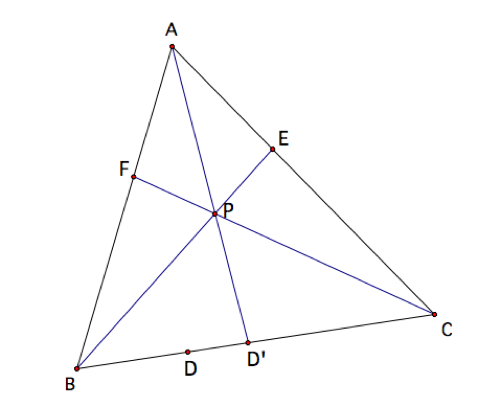
Since AD, BE and CF are concurrent, then we know from our assumption that
However, we assumed
.
Equating these two equations,
we obtain:
Thus, D=DÕ, which implies that AD, BE and CF are concurrent. Therefore, CevaÕs theorem holds.
CONCURRENCY OF THREE
MEDIANS
Suppose P is the centroid of triangle ABC.
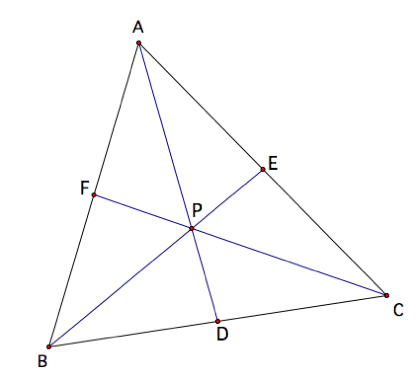
How could we use CevaÕs
theorem to prove concurrency of the medians? If we recall the definition of a centroid of a triangle, it is
the point of intersection of the triangleÕs three medians. In relating this definition to CevaÕs
theorem, this means that points D, E,
and F are the midpoints of
segments BC, AC, and AB respectively.
Hence, AF=FB, BD=CD, and CE=AE. Now,
CevaÕs theorem states that segments AD, BE and CF
are concurrent if and only if the product of the ratios
.
In substituting the values of
the aforementioned equivalent segments, we have
Therefore, since the ratio of
the products is one, then the three medians, namely AD, BE and CF, are concurrent.
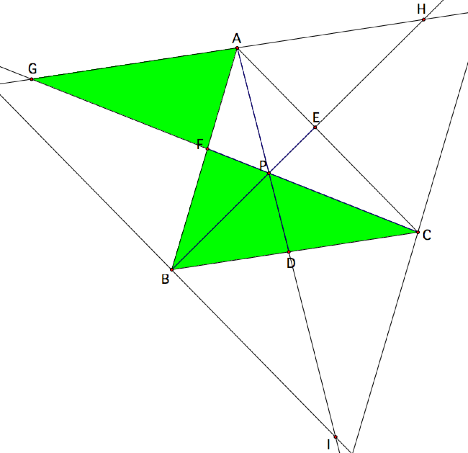
GENERALIZATION
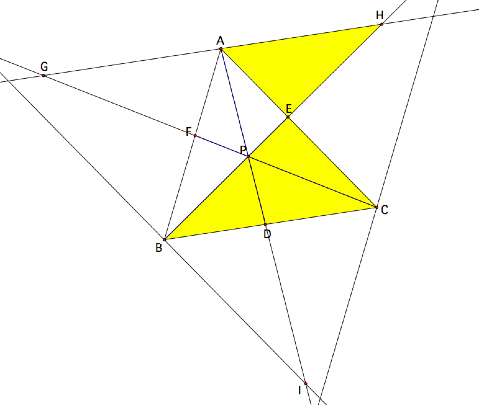
Suppose we want to explore a
generalization of CevaÕs theorem such that P can lie outside of triangle ABC. In
order for P to lie outside the
triangle, we must construct our diagram using lines rather than segments. Click HERE
to see a working GSP sketch of this case.
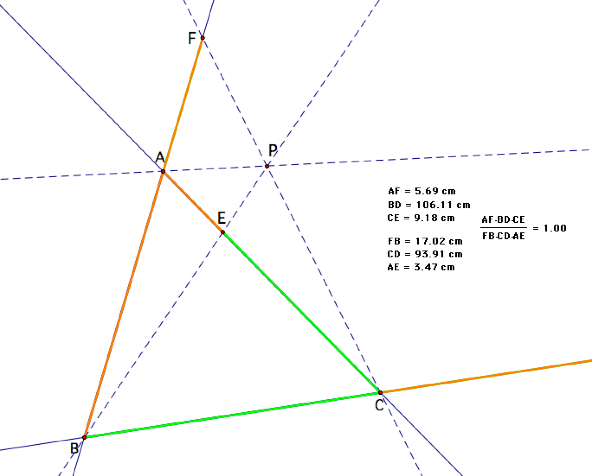
Therefore, we see from the
diagram and the GSP sketch that even when P is not contained within triangle ABC, CevaÕs theorem still holds since the ratio of the
products is still one.