Parametric Equations

By Colleen Garrett

I will begin this investigation by exploring x=acos(t) and y=bsin(t) for various a and b and for 0£t£2p.

Let’s see what happens when a=b.

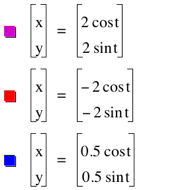
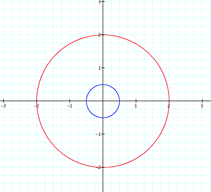
When a and b both equal 2 we get a circle with center at the origin and radius 2.

When a and b both equal -2 we get a circle equivalent to the circle when a and b both equal 2

When a and b both equal .5 we get a circle with center at the origin and radius .5.

gives us the radius of our circle centered at the origin.

What happens when a<b?

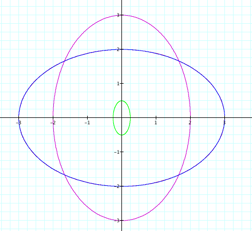
We can see here that we have ellipses. gives us the distance from the origin along the horizontal axis and gives us the distance from the origina along the vertical axis. Notice that if then the horizontal axis is the major axis of the ellipse.

What happens when a>b?

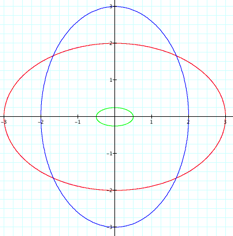
We can see here that we have ellipses. gives us the distance from the origin along the horizontal axis and gives us the distance from the origin along the vertical axis. Notice that if then the vertical axis is the major axis of the ellipse.

Now let’s investigate x=a(cos(t))² and y=b(sin(t))² for various values of a and b and for 0£t£2p.

Click here to watch a movie as a=b go from -5 to 5. This takes care of the case when a=b.

We get a line with slope equal to -1 which lies in the first quadrant when a and b are greater than 0 and lies in the third quadrant when a and b are less than 0.

Let’s now look at what happens when a<b.

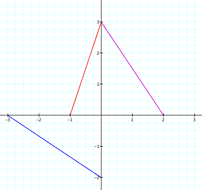
We can see that we get several lines. –b/a will give us the slope of the line. a gives us the x-intercept of the line and b gives us the y-intercept of the line.

What will happen if a>b?

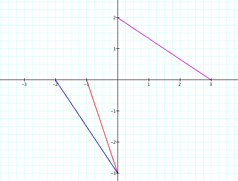
We can again see that we get several lines. Once again, –b/a will give us the slope of the line. a gives us the x-intercept of the line and b gives us the y-intercept of the line.

Let’s look at x=a(cos(t))³ and y=b(sin(t))³ for various values of a and b and for 0£t£2p.

Click here to watch a movie as a=b goes from -5 to 5. This takes care of the case when a=b.

We get a diamond shape with curved sides. As a and b increase the diamond shape gets larger and as they decrease the shape gets smaller.

What happens if a>b?

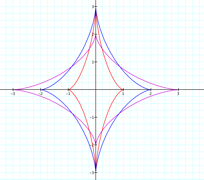
We have a and –a equal to the x-intercepts of the graph and b and –b equal to the y-intercepts of the graph.

What happens if a<b?

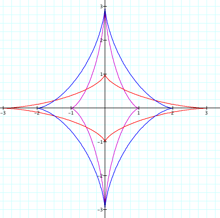
Once again we have a and –a equal to the x-intercepts of the graph and b and –b equal to the y-intercepts of the graph.

Let’s take a look at what happens if we keep increasing the power.

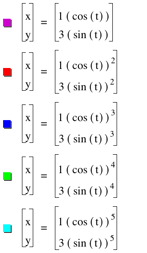
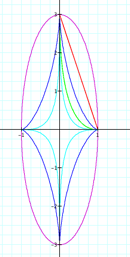
As the power of our equation decreases the graph approaches our ellipse!