Polar Equations

By Colleen Garrett

In this assignment I will investigate .

Let’s first look at when a=b and k is some integer.

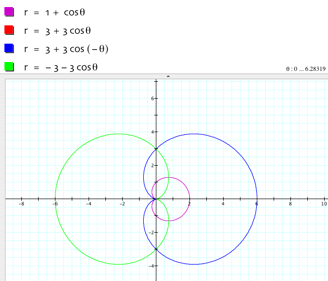
These shapes we have created are called cartiods. Notice that as the value of a and b increase the cartiod gets larger. Now look at the equations and . They are the same graph because cosine is an even function. You should also notice that when we change a and b to –a and –b the cartiod is reflected across the y-axis.

Now let’s look at the shapes we get when a<b and a>b!

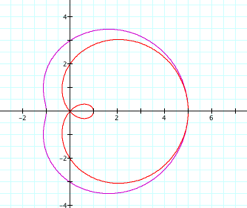
These shapes along with the cartiod are called limacons.

Now let’s explore what happens when a=0, b=1 and k is not equal to one.

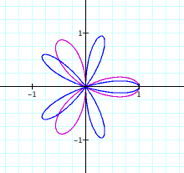
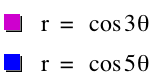
We no longer get a cartiod. We have a rose! We see that when k is odd represents the number of petals the graph will have.

What happens if k is even?

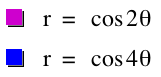
Now it appears that 2 represents the number of petals the graph will have.

What if we substitute sine in for cosine?

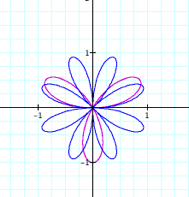
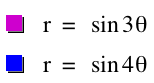
The same holds for sine as for cosine in regards to the number of petals. When k is odd represents the number of petals the graph will have and when k is even 2 represents the number of petals the graph will have.