Maximizing the Volume of a Box

By Colleen Garrett

To begin this exploration I constructed a lidless box with squares cut out of each corner using Geometer’s Sketchpad.

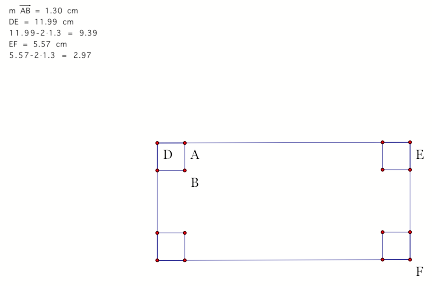Let us assume are given rectangle has length 8 units and width 5 units. If we let the height be our variable (x) we can deduce formulas for length and width:

Length=8-2x

Width=5-2x

Using an excel spreadsheet and examining the results, I claim the maximum volume of the box is 18 units cubed. With a volume equal to 18 units cubed, length=6 units, width=3 units, and height= 1 unit.

To verify my claim I graphed the equation y=x(8-2x)(5-2x) where x=height.

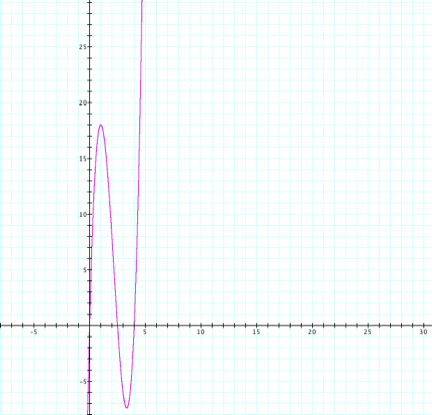
It is clear after examining the graph that the maximum value is 18.

Hence, the maximum volume of lidless box formed from a 5x8 sheet with a square removed from each corner is 18 units cubed.