Exploring Second Degree Equations

By Colleen Garrett

In this investigation I will construct graphs for the parabola y=ax²+bx+c for different values of a, b, and c.

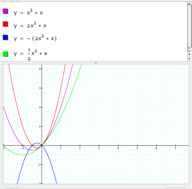
Let’s begin by altering a. Click on the link below to watch y=ax²+x as a varies from -5 to 5.

Altering a

For example, Let a=1/2 and 2. Notice that when a>1 the graph approaches infinity more rapidly and when 0<a<1 the graph approaches infinity less rapidly. Also note that when a is negative the graph is reflected across the x-axis.

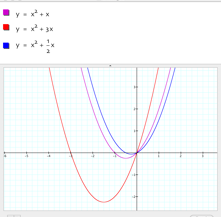
Now let’s alter b. For example, let b=3 and b=1/2. You can see that this alteration of b is causing the vertex of the parabola to shift.

Click on the link below to watch y=x²+bx as b varies from -3 to 3.

Altering b. You can see that the vertex of the parabola is moving along a parabolic curve as b changes. Let’s try and solve for this curve.

You know from the quadratic equation that the x-coordinate of our vertex is equal to -b/2a. Plugging in

x=-b/2a into our original equation y=x²+bx we get the following:

y=(-b/2a) ² + b(-b/2a)

=(b²/4)-(b²/2)

=(b²/4)-(2b²/4)

=-b²/4

=-x²

Hence, as b changes the vertex of y=x²+x moves along the curve y=-x².

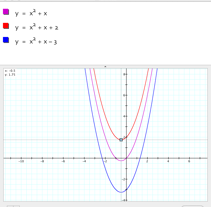
Now let’s alter c. Click below to watch the graph as c varies from -3 to 3.

Altering c.

You can see that altering c changes the y coordinate of the vertex of the parabola. If c>0 the graph moves up the y-axis, and if c<0 the graph moves down the y=axis.

For example, let c=2 and c=-3.