Exploring Quadratic Equations Keeping a and c Constant

By Colleen Garrett

In this investigation I will explore the graph y=ax²+bx+c for values of b equaling -3,-2,

-1,0,1,2,3 while keeping a and c constant.

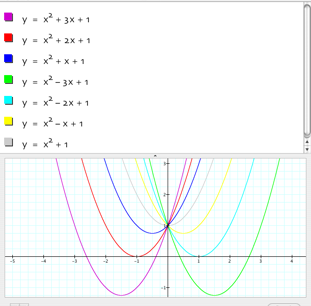
When =3 x has 2 real roots because the graph intersects the x-axis at 2 points.

When =2 x has 1 real root because the graph intersects the x-axis at 1 point.

When =1 x has no real roots because the graph does not intersect the x-axis at any point.

Now let’s consider the locus of the vertices of the set of parabolas graphed from y=x²+bx+1. We know that from the quadratic formula we get that the x-coordinate of the vertex is equal to –b/2a. Plugging this value you in for x in our equation y=x²+bx+1 we get that y-coordinate of the vertex equals (–b²/4)+1. We can put these values of x and y into a parametric equation to generate all vertices for all values of b in the equation y=x²

+bx+1.

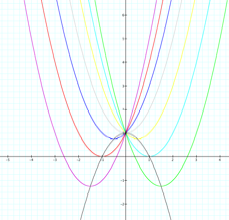
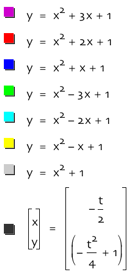
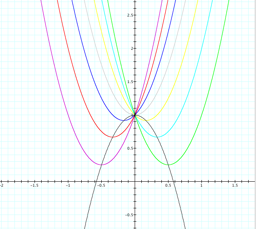
The black parabola created by the parametric equation is y=-x²+1.

Let’s look at a few more examples. y=3x²+bx+1 for values of b equaling -3,-2,-1,0,1,2,3.

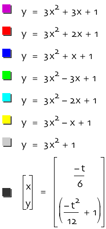
The locus of the vertices graphed from y=3x²+bx+1 is y=-3x²+1

What about y=-2x²+bx+1 for values of b equaling -3,-2,-1,0,1,2,3.

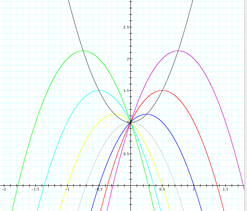
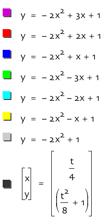
The locus of the vertices graphed from y=-2x²+bx+1 is y=2x²+1

Let b=0 in each of our examples. We get the following equations:

y=x²+1

y=3x²+1

y=-2x²+1

Now take a look at the locus of vertices from all three of these equations

y=-x²+1

y=-3x²+1

y=2x²+1

You can see that the value for c does not change and that the value of a changes to –a.

This helps us to conclude that the locus of vertices generated by a function when b=0 is y=-ax²+c