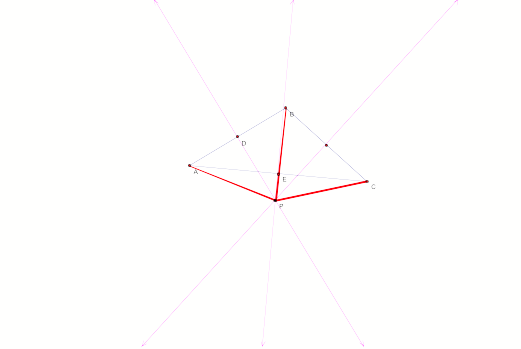
Proof of Concurrence of the Perpendicular Bisectors of
a Triangle.
By Colleen Garrett
Given: Triangle ABC. Claim: The perpendicular
bisectors of Triangle ABC concur at point P. Construct the perpendicular
bisectors of two sides of the triangle.
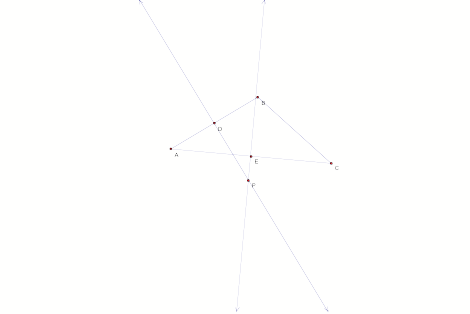
Construct PB and PA and
PC. Point P is equidistant from
points A and B because points lying on the perpendicular bisector are
equidistant from the segments endpoints. Hence PB![]() PA. Similarly, PC
PA. Similarly, PC![]() PA.
PA.
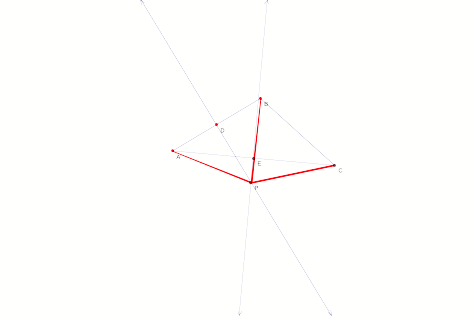
By transitivity, PC![]() PB therefore, P is equidistant from points B and C. P then lies on the perpendicular
bisector of segment BC. Hence, the
perpendicular bisectors of a triangle concur at point P.
PB therefore, P is equidistant from points B and C. P then lies on the perpendicular
bisector of segment BC. Hence, the
perpendicular bisectors of a triangle concur at point P.