Tangent Circles

By Colleen Garrett

In this assignment I will construct a GSP tool for tangent circles and explore different types of loci.

We have three different cases of tangent circles. Click here for a GSP tool that can be used to explore all three cases.

Case 1: One circle lies inside of the other.

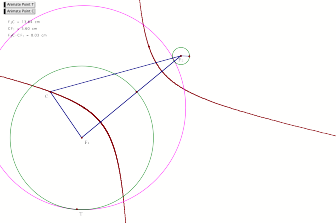
What do we get if we construct the locus of the center of the tangent circle(pink circle)?

Find out by clicking here and animating point T.

It appears that we have constructed an ellipse. Can we prove this?

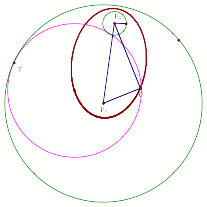
We know that by definition an ellipse is the set of all points P in the plane such that the sum of the distances from P to two fixed points is a given constant.

Our foci(fixed points) will be the centers of our original circles. Choose a point C on the “ellipse.” Click the picture below to see if the sum of the distances from C to the foci remains constant.

You should find that the sum does remain constant. Therefore, we have an ellipse!

Case 2: The two circles intersect.

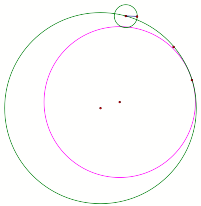
What do we get if we construct the locus of the center of the tangent circle(pink circle)?

Find out by clicking here and animating point T.

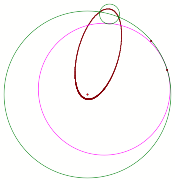
Once again it appears we have an ellipse. We can prove that we do have an ellipse in a similar manner as shown in Case 1.

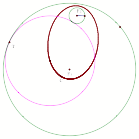
Case 3: The two circles are disjoint

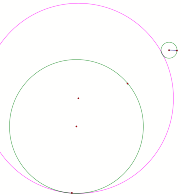
What do we get if we construct the locus of the center of the tangent circle(pink circle)?

Find out by clicking here and animating point T.

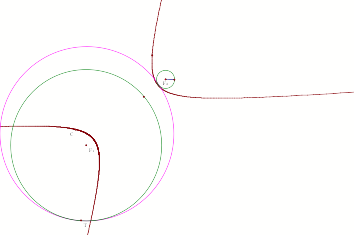
This time it appears that we get a hyperbola. Can we prove this?

We know that by definition a hyperbola is the set of all points P in the plane such that the difference of the distances from P to two fixed points is a given constant.

Our foci(fixed points) will be the centers of our original circles. Choose a point C on the “hyperbola.” Click the picture below to see if the differences of the distances from C to the foci remains constant.

You should get that the difference remains constant. Therefore, we have a hyperbola!