Orthocenters and Circumcenters

By Colleen Garrett

I will begin this investigation by first doing the following:

1. Construct any triangle ABC.

2. Construct the Orthocenter H of triangle ABC.

3. Construct the Orthocenter of triangle HBC.

4. Construct the Orthocenter of triangle HAB.

5. Construct the Orthocenter of triangle HAC.

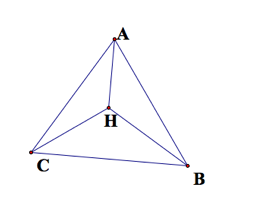
When constructing the orthocenters of the small triangles we get that the orthocenter of DHCB=A, orthocenter of DHAB=C, and the orthocenter of DHAC=B.

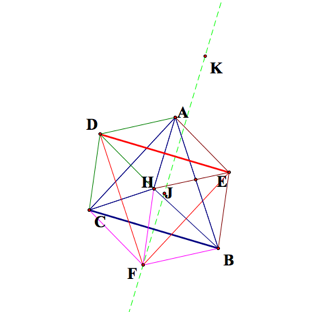
Now let’s construct the circumcircles of triangles ABC, HBC, HAB, and HAC.

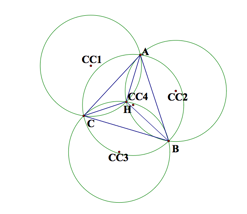
CC1, CC2, and CC3 are circumcenters of the small triangles.

Let’s hide the circumcircles and construct segments connecting the circumcenters of the small triangles. Let CC1=D, CC2=E, CC3=F, and CC4=J. We have a new triangle DFDE. Constructing the circumcircle of DFDE we see that it has circumcenter H. (Recall: H is the orthocenter of our original DABC).

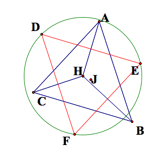
Hide the circumcirlce of DDFE.

Claim: DFDE@DABC.

Proof:

Connect circumcenter F to points C,H, and B. Connect circumcenter D to points C, H, and A. Connect circumcenter E to points A,H, and B.

, , and because we know that the circumcenter of a triangle is equidistant from the vertices of the triangle.

We also know that H is the circumcenter of DDFE so .

Therefore, by transitivity . The result we will be using is .

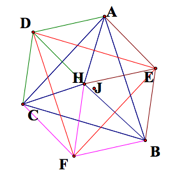
Now construct a line perpendicular to through point F. Since , F is equidistant from point C and point B; therefore, F must lie on the perpendicular bisector of . Hence, if perpendicular to as well. Two lines that are perpendicular to the same line are parallel; therefore, .

Now construct . We know have two triangles, DDEB and DDCB.

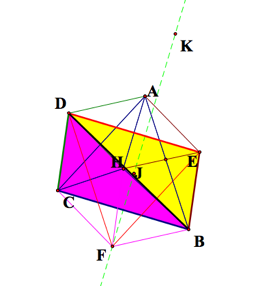
Recall that . is a transversal intersecting parallel lines and therefore ÐCDBÐEBD by alternating interior angles. Also . We now have DDEBDDCB by SAS.

Now by CPCTC . By a similar argument and . Hence DFDE@DABC by SSS.