Pedal Triangles

By Colleen Garrett

In this investigation I will explore how pedal triangles change as P moves to the orthocenter, circumcenter and incenter of the original triangle.

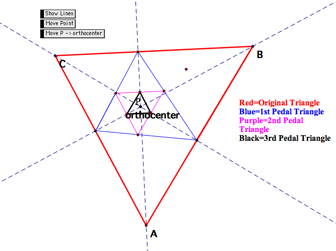
Let’s first look at what happens when P moves to the orthocenter.

Click here!

The vertices of the 1^st pedal triangle are the feet of the altitudes of the original triangle, thus the 1^st pedal triangle is also the orthic triangle of the original.

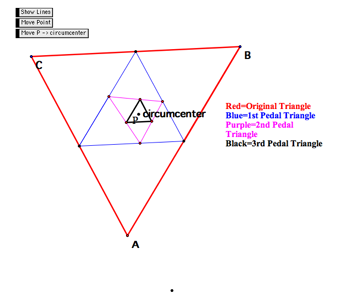
Now let’s move P to the circumcenter! Click here!

The vertices of the 1^st pedal triangle happen to be the midpoints of segments AB, BC, and CA, thus the 1^st pedal triangle is also the medial triangle.

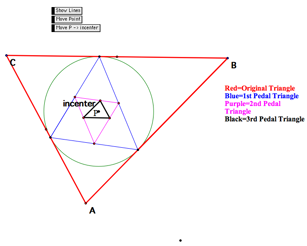
Now let’s look at what happens when P is the incenter. Click here!

If we construct the circumcircle of the 1^st pedal triangle we can see that P has become the circumcenter of the 1^st pedal triangle.

Can we show that the third pedal triangle is similar to the first?

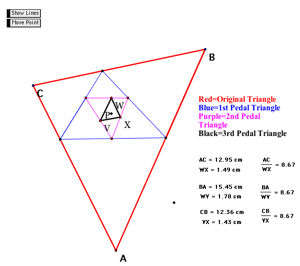
Using Geometer’s sketchpad to calculate the ratio of the sides of the original and 3^rd pedal triangles we see that the corresponding sides have the same ratio thus, our original triangle is similar to the 3^rd pedal triangle.