Final Project

By Colleen Garrett

A. Bouncing Barney. We discussed this investigation in class. Your challenge now is to prepare a write-up on it, exploring the underlying mathematics ideas and conjectures.

Barney is in the triangular room shown here. He walks from a point on BC parallel to AC. When he reaches AB, he turns and walks parallel to BC. When he reaches AC, he turns and walks parallel to AB. Prove that Barney will eventually return to his starting point. How many times will Barney reach a wall before returning to his starting point? Explore and discuss for various starting points on line BC, including points exterior to segment BC. Discuss and prove any mathematical conjectures you find in the situation.

The picture below shows that if we continue in the same manner as above having Barney walk along parallels he will eventually get back to his starting point.

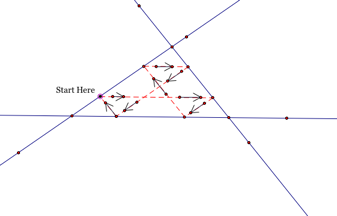
Let’s take a look at how far Barney is walking!

Case 1: Barney begins on a vertex of the triangle.

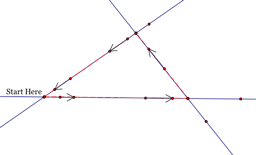
If Barney starts at a vertex of the triangle he walks the perimeter of the triangle!

Will Barney always walk the perimeter of the triangle regardless of his starting point?

Case 2: Barney begins at the midpoint of a side of a triangle.

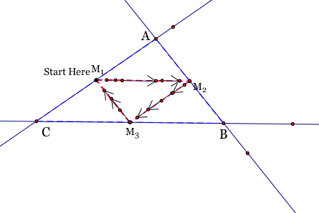
=, =, and = because , , and are mid-segments of DABC.

Therefore, Barney walks a distance equivalent to ++= which is half the perimeter of DABC.

Case 3: What if Barney starts at a point on a side of DABC which is not a vertex? How far will Barney walk?

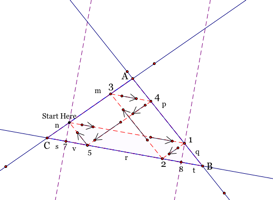
We can show that each path is equal to a part of a side of DABC. For our purposes let the Start Here point=S.

Examining parallelogram C345 we get . Examining parallelogram A45S .

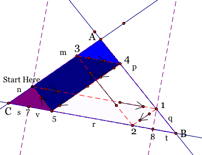
Examining parallelogram S1b5 we get . Examining parallelogram S12C we get .

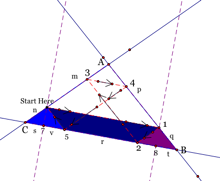
Examining parallelogram A123 we get . Examining parallelogram S187 we get .

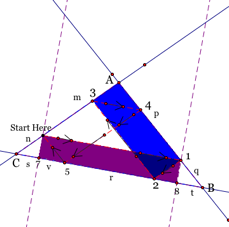
Since v is contained in r we have 2v and t still needs to be accounted for. We need to show v@t. We can do this by showing DS57@D1B8.

We know that and that ÐS75@Ð18B (both equal 90° by construction). Parallelogram S187 tells us . We now have DS57@D1B8 by hypotenuse leg. Hence, v@t by CPCTC.

Now substituting t for one v we get the paths

equals the perimeter of DABC. Thus, if Barney begins at a point on the side of the triangle, which is not the vertex, he will walk the perimeter of the triangle.

Case 4: What if Barney starts at a point outside DABC? How far will Barney walk?

Once again let the point Start Here=S. First we will show that DA43@DB21@D5CS.

Figure1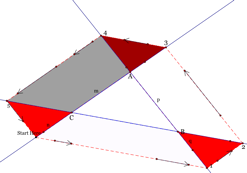

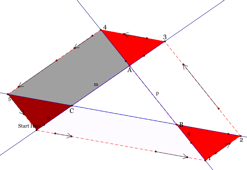
Figure 2

Looking at the parallelogram in Figure 1 we see that and looking at Figure 2 we see that . Using similar arguments we can conclude and . We still need to show that the third side is @. Look at Figure 3 below.

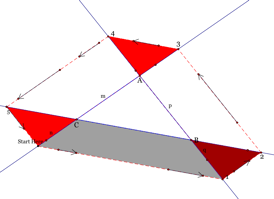
Figure 3

Using the gray parallelogram we can conclude . Similarly using other parallelograms we can conclude that . We now have DA43@DB21@D5CS by SSS.

We have three grey parallelograms 54AS, 321A, and 5B1S.

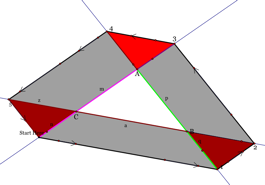
Using these parallelograms (opposite sides are congruent) we can conclude that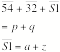

Now we can calculate the distance Barney walks.

Distance=

Substituting we get Distance=. Observe that =perimeter of little red triangle and that =perimeter of DABC.

We know have Distance=perimeter of DABC+ perimeter of little red triangle+ . Oh, but look =the perimeter of little red triangle too.

Hence, the Distance Barney walks when he begins outside the triangle= perimeter of DABC+ 2(perimeter of little red triangle).

B. Ceva's Theorem. Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively.

1. Explore (AE)(CD)(FB) and (EC)(DB)(FA) for various triangles and various locations of P. Click here to explore!

We notice that regardless of the location of P inside the triangle (AE)(CD)(FB)= (EC)(DB)(FA)Þ . This result is Ceva’s Theorem.

Ceva’s Theorem: If three cevians AC, CF, BE, one through each vertex of a DABC, are concurrent then .

Proof: Begin by drawing in parallel lines.

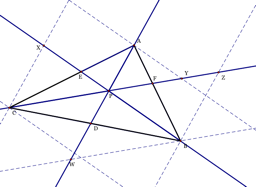
We now have several sets of similar triangles.

DAFP~DZFB because ÐAFP and ÐZFB are congruent by vertical angles and, ÐFAP and ÐFBZ are congruent by alternating interior angles.

DEXC~DEAP because ÐAEP and ÐXEC are congruent by vertical angles and, ÐEXC and ÐEPA are congruent by alternating interior angles.

DCDP~DWDB because ÐCDP and ÐWDB are congruent by vertical angles and, ÐDPC and ÐDWB are congruent by alternating interior angles.

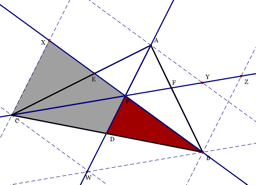
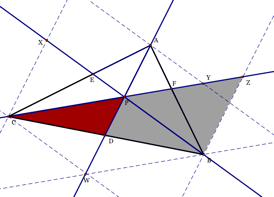
DXBC~DPDF because ÐBXC and ÐXPA are congruent by alternating interior anglesÞ ÐBXC@ÐDPB and ÐXBC@ÐPBD.

DZBC~DPDC because ÐBZC and ÐZPA are congruent by alternating interior anglesÞ ÐBZC@ÐDPC and ÐZCB@ÐPCD.

These 5 pairs of similar triangles get us the following proportions:

DAFP~DZFBÞ

DEXC~DEAPÞ

DCDP~DWDBÞ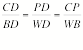

DXBC~DPDFÞ

DZBC~DPDCÞ

Now we can show that using substitution.

=and = so we now have AP will cancel leaving us

with . Now. Recall, and

. Substituting we get

=1. Therefore, we have shown .

Explore a generalization of the result (using lines rather than segments to construct ABC) so that point P can be outside the triangle. Show a working GSP sketch.

Click here to explore!

It appears that when P is outside the triangle Ceva’s Theorem is true!