Gayle Gilbert

Problem 1: For any triangle, construct a segment parallel to a base of the triangle that divides the triangle into two equal areas.

Before we start constructing, let’s see if we can find a ratio of the corresponding sides of the similar triangles where the areas are in ratio of 1:2.

Let the triangle be labeled as follows:

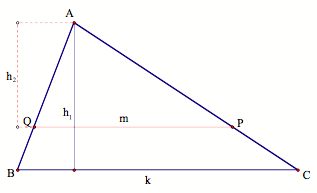
Because PQ is parallel to BC, triangle AQP is similar to triangle ABC. The coefficient of similitude gives the equality

The relationship of the areas of the two triangles gives

Dividing both sides by h₂ gives

By substitution,

Now we can see the ratio of the sides. Let’s construct a segment of length m parallel to the base of length k to divide the area of the triangle in half.

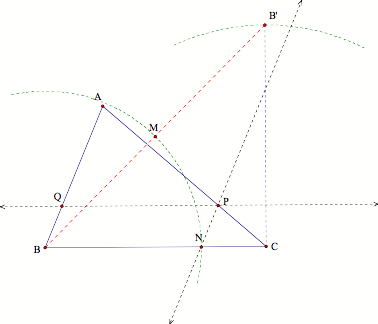
Now we are ready to begin constructing. Take any triangle ABC. Construct a segment B'C of length BC and perpendicular to BC at C. Draw B'B.

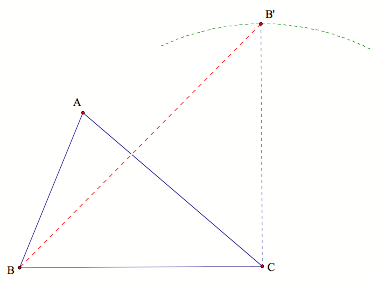
Find the midpoint M of BB'. Mark an arc of radius MB with center at B to intersect the segment BC at point N.

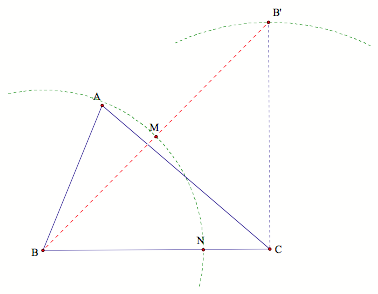
Now, construct a line parallel to AB through N. This line will intersect AC at P and a parallel line to BC through P will intersect side AB at Q. PQ is the desired segment that divides the original triangle into equal areas.

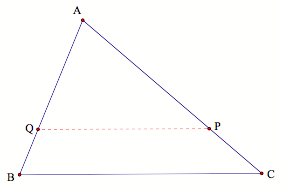
The area of AQP is half the area of ABC. Notice also that the area of quadrilateral BQPC must equal to the area of AQP.

Follow this link for a GSP construction, which also contains a GSP tool that you can use.

Problem 2, Part A: If the parallel segment that divides the triangle into two equal areas is drawn for each base, a smaller triangle is formed. What is the ratio of the area of the small triangle to the original?

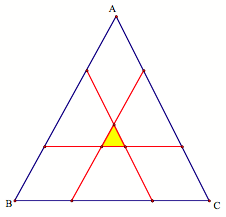
Since we have parallel lines, then by AAA, the small yellow triangle is similar to triangle ABC. By investigations in GSP, I have found that the ratio between the small triangle and the large triangle is approximately 0.01472. Click this GSP link to investigate for yourself.

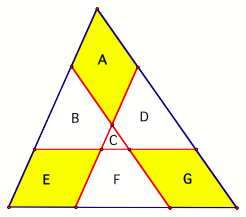
Problem 2, Part B: What is the ratio of the area of the shaded triangle to the area of the original triangle in the figure below? Here again the segments parallel to the bases divide the original triangles into two equal areas.

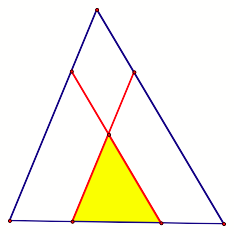
Again, by AAA, the yellow shaded triangle is similar to the original triangle. By investigations in GSP, I have found that the ratio between the shaded triangle and the large triangle is approximately 0.1716. Click this GSP link to investigate for yourself.

Problem 2, Part C: Prove that the measures of the three shaded areas in each of the figures below are the same. In each figure what is the ratio of the area of one of the regions to the area of the original triangle?

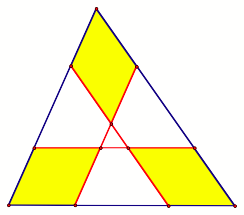
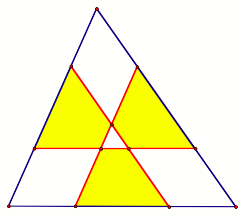
Let’s label each of the figure spaces A-G as follows:

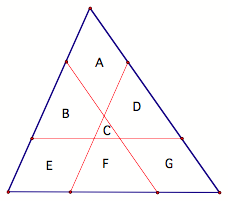
Thus, by the principle of halving the area, we know that:

By regrouping and simplifying, we find that (1):

This can be represented in the following picture:

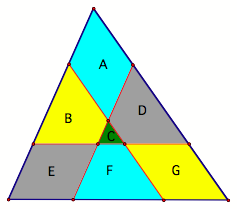
To prove that A=E=G, we must first see that they are all parallelograms. Since the ½ areas are made by lines parallel to the base, then they are obviously parallelograms. Let’s label the points of our picture.

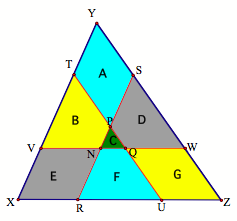
We know that XR = SY since RS || XY, TY = UZ since TU || YZ, and WZ = XV since VW || XZ. Therefore, figures A, E, and G are actually rhombuses with equal area (A = E = G). By substitution into our previous equations (1), we see that B = D = F as well. Therefore, we have proven the three shaded areas in the figures are equal.

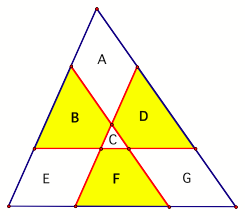
The ratio of a single trapezoid region, like F, is the ratio of the region in Part C minus the small triangle in Part A. So, the ratio is approximately 0.1569. Thus, the ratio of all three is approximately 3*0.1569=0.4706. Click this GSP link to investigate.

Thus, the ratio of the rhombus regions (A, E, G) over the entire triangle is 1-0.4706-.0.01472=approximately 0.5147. Click this GSP link to investigate.

Return