How Wide is the Alley?
by
Gayle Gilbert
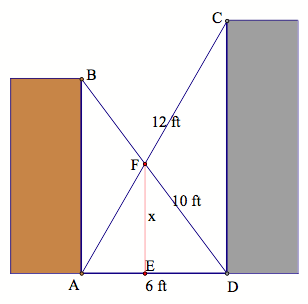
Problem 1: A 6-foot wide alley has both walls
perpendicular to the ground. Two ladders, one 10 feet long, the other 12 feet,
are propped up from opposite bottom corners to the adjacent wall, forming an X
shape. All four legs of each ladder are firmly touching either the bottom
corner or the opposite wall. The two ladders are side by side and also touching
each other at the intersection of the X shape. What is the distance from the
point of intersection to the ground?
First, letŐs
label all the points of intersection.
See the picture below:
Since 
and 
are right
triangles, we can use the Pythagorean Theorem to find AB and DC.
Notice by AAA, 
and 
, so we can use ratios to solve for x:
Since 
, then we can substitute 
for 
in the second
equation.
Now, letŐs set
the equations equal to each other and solve for x.
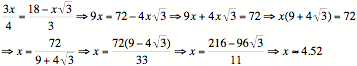
Thus, the ladders
intersect at approximately 4.52 feet off the ground.
LetŐs change the situation
a little bit and see if we are able to figure it out the missing information
still. LetŐs say we know the
distance of the point of intersection to the ground. This time we want to find how wide the alley is. Look at the following situation.
Problem 2: Two buildings are separated by an alley.
Two ladders are placed so that the base of each ladder is against one of the
buildings and reaches the top of the other building. The two ladders are 40
feet and 30 feet long. Further, they cross at a point 10 feet from the ground.
How wide is the alley?
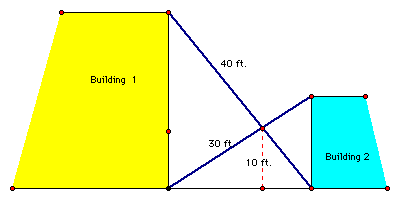
First, letŐs
label all the intersection points, like we did in the previous problem. However, this time we will put it on a
coordinate system.
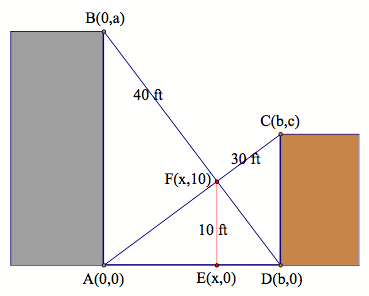
LetŐs use the
Pythagorean Theorem for 
and 
to solve for the
heights of the two buildings.
For 
: 
For 
: 
Since we are putting
this situation on a graph, then we can derive the formulas for the two
ladders.
The equation for the 40-foot ladder is 
.
The equation for the 30-foot ladder is 
.
To find the point
where the two ladders intersect, we can just set the two equations equal to
each other.
LetŐs substitute
this value of x into
the second equation.
Since we know 
, 
, and 
, we can plug in these values to find b, or the width of the
alley.
To solve for x,
letŐs graph this equation.
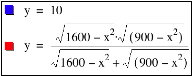
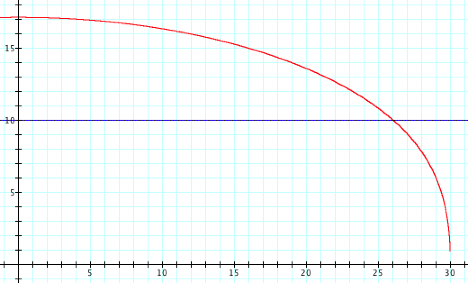
When we trace the
graph, we see that the two graphs intersect at (26.0329,10), so the alley is
approximately 26.03 feet wide.
If we continue to
solve, we can see that the height of the first building is approximately
30.3692 feet, the height of the second building is approximately 14.9093 feet,
and the distance from B to C is approximately 30.2774. These lengths yield a trapezoid with
diagonals of lengths 30 and 40 feet such that the distance from the
intersection of the diagonals to the base is 10 feet.