Trisections of the Areas of Triangles
by
Gayle Gilbert
Problem 1:
Given a
triangle ABC, find a point D such that line segments AD, BD, and CD trisect the
area of the triangle into three regions with equal areas.
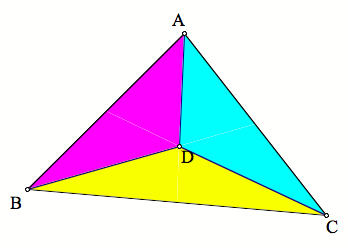
Before
we look at when it is in the interior of the triangle, letÕs first investigate
what happens when point D is on the triangle. When D is on the triangle, only two lines will be formed to
trisect the triangle. LetÕs look
at the following scenarios:
Base
Case: First, letÕs look at what happens when point D is on the vertex of
the triangle. If D is on a vertex,
letÕs say D=A, then to trisect the area, we must trisect the opposite side
(segment BC here). By connecting A
to the trisection points of BC, then we will have three triangles that are a
third of the area of the original triangle ABC. We can see this because the heights of all these triangles
are the same, and we just constructed their base lengths to be the same. See the picture below or you can see
the following GSP sketch.
Case
One: Now, letÕs look at what happens when point D is on the side of the
triangle (letÕs say on BC) at a trisection point. If this happens, then we can just connect D to the opposite
vertex (here A). We know this is a
third of the area of the original triangle because the height is the same and
the base is a third of the original.
Now, we have two-thirds of the area of the original triangle
remaining. If we just bisect this
triangle on any of its sides from any of its vertices (A, B, or D), then the
areas of these two triangles will also be equal to one third of the original
triangle. The following triangles
are the three different possibilities when point D falls on the trisection point
on BC closest to C.
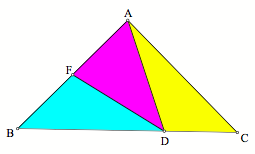
Case
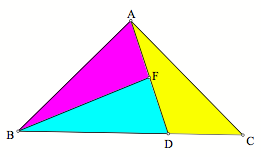
Two: Finally, letÕs look at what happens when point D is on any point on
the side of the triangle other than the trisection point or vertex (here weÕll
say BC). First, weÕll need to
construct a triangle, which is one-third the area of triangle ABC. Then, weÕll need to bisect the
remaining two-thirds portion of the triangle. If the point is to the left or right of the altitude, then
the construction will look somewhat like the picture on the left, although if
it were on the right side, then it would mirror this image. If the point is equal to the
intersection point of the altitude of A with side BC, then the picture will
look like the right picture.
Please see the following GSP links to see the construction of the area trisection
for the left, center, and right cases.
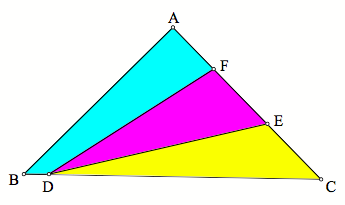
Case
Three: Now that we have seen how to trisect the area of a triangle when
point D is on the triangle, now letÕs look at how to trisect the area of a
triangle when point D is on the interior of the triangle, like the initial
question implies. My claim is that
when D equals the centroid of triangle ABC, this is the point at which such line
segments AD, BD, and CD trisect the area of a triangle into three regions with
equal area. To prove this, letÕs
construct triangle ABC and its medians such that D is the centroid of the
triangle.
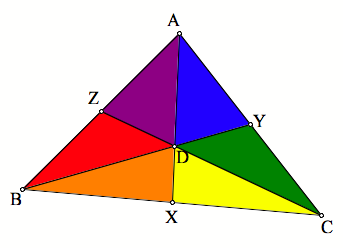
Notice
that the area of 
the area of 
, and weÕll say the area is 
, because they have the same base length and height. Likewise, the area of 
the area of 
(which weÕll say
the area is 
), and the area of 
the area of 
(which weÕll say
is 
).
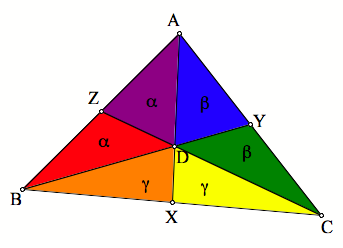
Also,
we know that the medians of a triangle cut the area of that triangle in half,
so 
. Thus, 
. Therefore, we
know that each of these triangles is equal to 1/6 of the area of the original
triangle. Therefore, the area of 
the area of 
the area of 
the area of 
. Thus, when
point D is the centroid of any triangle ABC, then the segments DA, DB, and DC
trisect the area of the triangle into three regions with equal area.
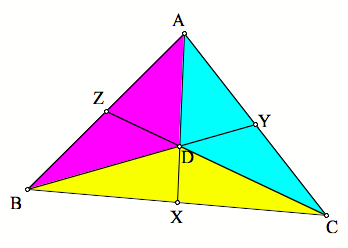
Q.E.D.
Problem 2:
Given a triangle
ABC. Construct two line segments parallel to the base BC to divide the triangle
into three regions with equal areas.
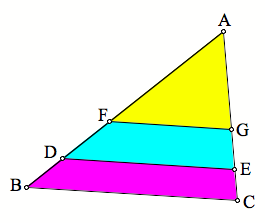
Well, we know that 
will be 2/3 the
area of 
. Since 
is 1/3 the area
of 
, then 
is ½ the
area of 
. From Essay 1, we
know how to bisect the area of a triangle with a line parallel to the base, so
if we can just construct a segment DE such that it is 2/3 the area of 
, then we will be able to trisect the area of the triangle
with two segments parallel to the base.
LetÕs compare the areas of 
and 
.
Notice that the heights of
the triangle are proportional to the sides of the triangle, so we can
substitute 
into the equation.
Now, we can see that the
sides of DE is 
times the length
of BC. We can just construct 
and then trisect
it. To construct 
, we must create a spiral coming off of BC. Each of the triangles coming off 
are right
triangles and the outer leg is always the same length as BC.
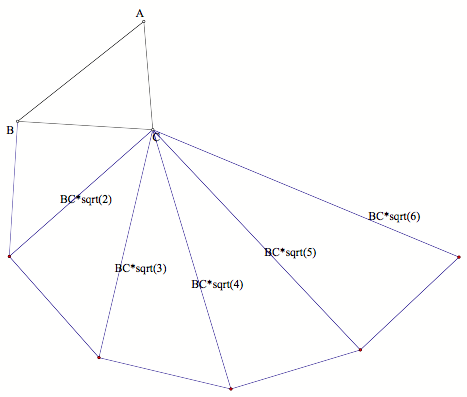
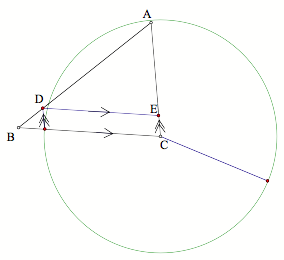
Now, we just have to trisect 
, and then we can construct a circle centered at C with a
radius of 
. The distance
between C and the point of intersection between the circle and BC is 
. We just need
to translate the distance up so that we have 
with area 2/3 of
. To do this, we
can just create a parallelogram.
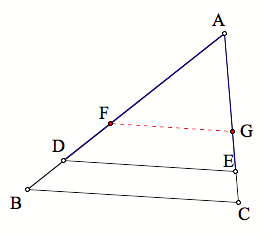
Now, all we have to do is
bisect 
using the
methods discussed in Essay 1.
Click this link to use a GSP tool.