Gayle Gilbert

Let’s evaluate the graph of y=a sin(bx+c) for different values of a, b, and c in order to determine how different values of a, b, and c affect the graph. First, let’s evaluate the basic sine function, y=sin(x), where a=1, b=1, c=0.

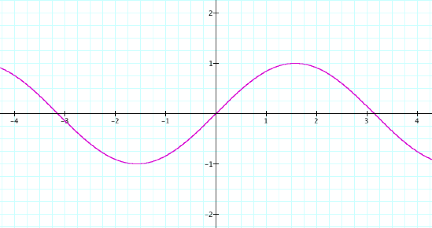
Now, let’s see how the graph will change when we change the a value but keep b=1 and c=0 constant. Let’s graph a=1, a=2, a=-1, a=½. Here’s the graph of y=sin(x) (purple), y=2sin(x) (red), y=-sin(x) (blue), and y=½sin(x) (green).

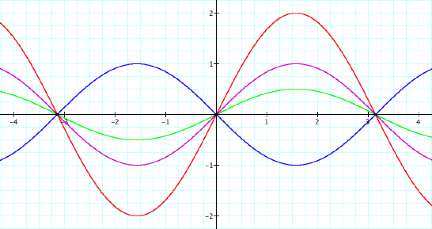
How does the graph change as a changes? A seems to change the maximum height of the graph. When a=2, the maximum height of the graph is 2. When a=½, the maximum height is ½ on the graph. When a is negative, it reflects the graph about the x-axis. We see here that the absolute value of a is the amplitude of the sine graph.

Now, let’s look at how the graph changes as the values of b change. We will keep a=1 and c=0 constant, but we will let b=1, b=2, b=-1, and b=½. Here’s the graph of y=sin(x) (purple), y=sin(2x) (red), y=sin(-x) (blue), and y=½sin(x) (green).

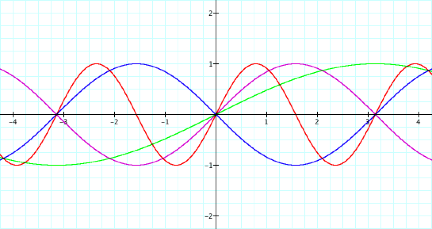
How does the graph change as b changes? When b increases, it seems to compress the sine function; when b increases, it seems to stretch the sine function; when b is negative, it seems to reflect the sine function about the x-axis. The period (how long it takes for the graph to repeat itself) for the normal sine function (purple) is 2*pi. When b=2, the period is ½(2*pi)=pi. When b=1/2, the period is 2(2*pi)=4pi. The period is two pi divided by the absolute value of b.

Now, let’s keep a=1 and b=1 constant but change the c value. We’ll look at c=0, c=1, and c=-1. Here’s the graph of y=sin(x) (purple), y=sin(x+1) (red), and y=sin(x-1) (blue).

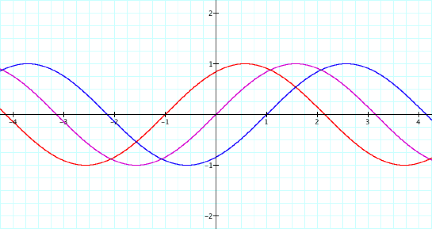
How does the graph change as c changes? There is a phase shift to the left when c is positive and a phase shift to the right when c is negative. The phase shift is equal to the -c/b.

How do you expect the graph of y=2sin(2x+2) to look? Well, we know the amplitude is 2, the period is 2pi/2=pi, and the phase shift is -2/2=-1. From this information, we have an idea of what the graph should look like. Let’s check. Here, I’ve graphed the basic sine function y=sin(x) in purple with the function y=2sin(2x+2) in green.

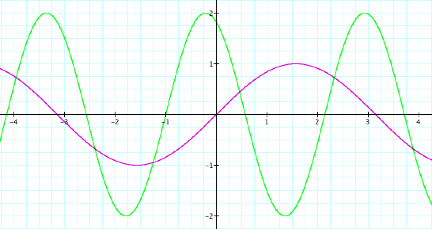
Notice, the amplitude is a=absolute value(2)=2, the period is 1/2(2pi)=pi, and the phase shift is to the left 1.

Let’s try another one. How would you expect the graph of y=-sin(-x) to look? Well, since a=-1, we are going to reflect the graph about the x-axis, and since b=-1, we will reflect the graph about the x-axis again, so this should look the same as y=sin(x). Let’s graph it to find out.

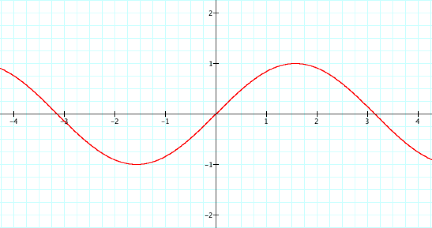
This is the same graph as the original y=sin(x) function, so our investigative work seems to hold true.

Let’s try one more. How would expect the graph of y=½sin(2x-1) to look? Well, a=1/2, so we would expect the graph to have an amplitude of ½, b=2, so we expect a period of 2*pi/2=pi, and c=-1, so we expect a phase shift of –(-1/2)=1/2.

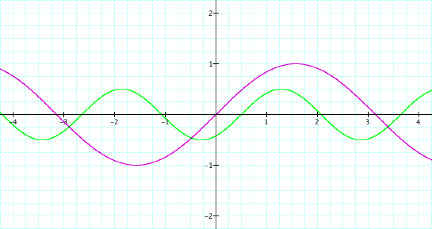
From the graph, we can see that we are correct. The amplitude is ½, the period is pi, and the phase shift is ½ to the right.

In conclusion, the amplitude is the absolute value of a, the period is 2*pi/absolute value of b, and the phase shift is –c/b.

Return