
Concurrency
of Angle Bisectors of Triangles
by
Gayle Gilbert & Greg Schmidt
Theorem: The three angle bisectors of the internal angles of a triangle are concurrent.
Proof of Theorem:
Let ABC be an arbitrary triangle. We begin by constructing the angle bisectors of A and C. Denote the intersection of the angle bisectors P.
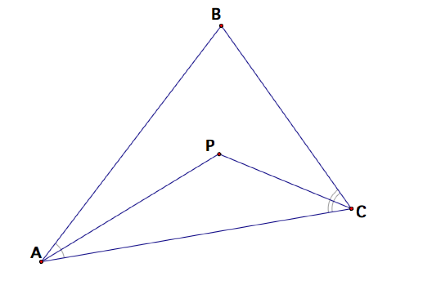
Next we construct segment BP.
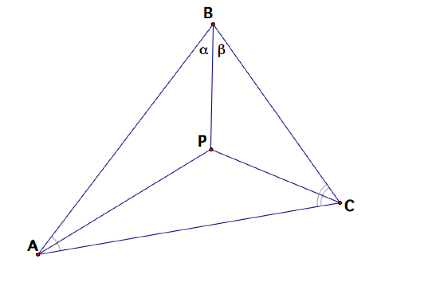
We claim that a = b.
Proof of Claim:
Construct perpendicular line segments from P to AB, AC, BC.
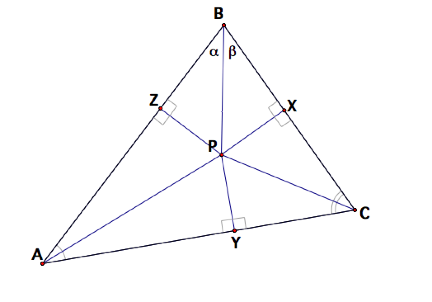
We note that APY is congruent to APZ, by hypotenuse-angle. Hence, PY is congruent to PZ since corresponding parts of congruent triangles are congruent. Now a similar argument shows that triangle CPY is congruent CPX, which shows that PY is congruent to PX. Whereby it immediately follows by substitution that PZ is congruent to PX.
Now we note that triangle PBZ is congruent to PBX by hypotenuse-leg. Thus is follows that a = b, since corresponding parts of congruent triangles are congruent.
Therefore, PB is an angle bisector of B, and intersects the angle bisectors of A and C at the same point P.
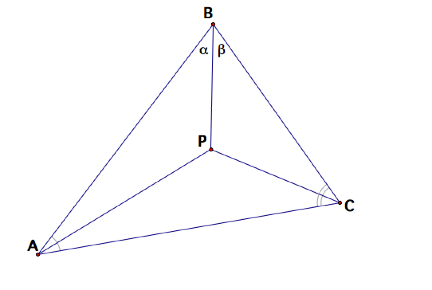
Q.E.D.