Altitudes and an OrthocenterÉand ratios which sum to oneÉor two!
by

 Gayle Gilbert & Greg Schmidt

 

Consider an acute triangle .  Let  denote the orthocenter and let , ,  be the feet of the perpendiculars of , , and  respectfully.

 

 

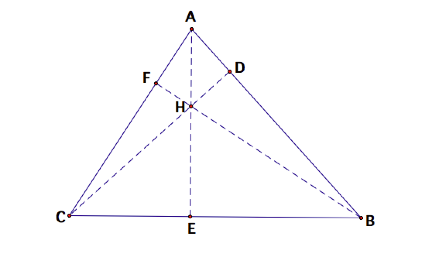
Then:

 

,

 

and

 

 

Proof:

 

Let , , ,  represent the area of , , and  respectfully.  So we have that

 

 

 

,

 

,

 

,

 

 

 

Now we also have that

 

 

                                                                                   

              

                                                                                               

                                               

               

 

 

 

                   (By substituting previous values of , , , )

 

 

 

Now we note that:

 

(1)

 

(2)

 

(3)

 

 

 

By substituting each new altitude representation into our previous result gives us

 

 

 

 

 

 

 

Which is what we wanted!

 

Notice if  is an obtuse triangle our relation no longer holds since the orthocenter  lies outside the triangle .

 

 

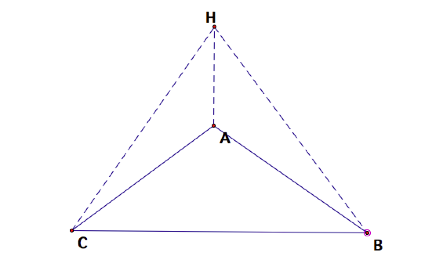
Nevertheless, we can now consider the triangle , which has orthocenter , thereby reducing to the previously proven case!

 

Return