A
Pedal Triangle and the Simson Line
by
Gayle Gilbert & Greg Schmidt
Let 
be any
triangle. Now let 
be a point,
which is not one of the vertices 
, 
, 
. Drop
perpendiculars from 
to the three
sides of the triangle. Next, label
the intersection of the lines from 
with the sides 
, 
, 
, as 
, 
,
, respectively.
Then the triangle 
is called the
pedal triangle.
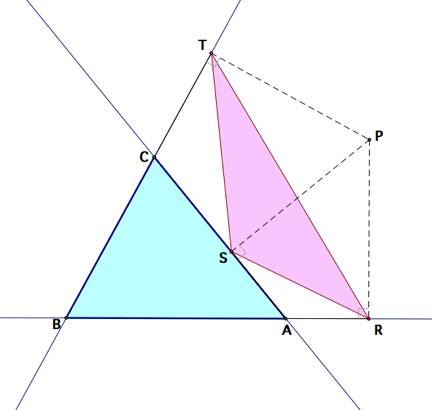
We will examine the special case where the point 
lies on the
circumcircle of 
. In this case
the feet of the perpendiculars drawn from 
to the sides 
, 
, 
are collinear,
which is called the Simson Line.
We will prove this is true.
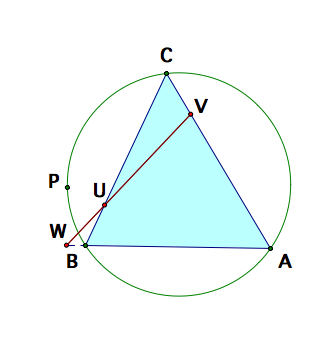
Proof:
Now, since 
is perpendicular to 
and 
is perpendicular
to 
, we have that the point 
must lie on the
circumcircle of 
.
We can employ similar arguments to show that 
lies on the
circumcircle of 
as well as the
circumcircle of 
.
From this we have that 
, 
, and 
are all cyclic
quadrilaterals.
So from the fact that 
is a cyclic
quadrilateral we have that,
which in turn tells us that
But 
is also a cyclic
quadrilateral, and so we have
Now, opposite angles in a cyclic quadrilateral are supplementary and so it follows that
Next we need only subtract 
and we have
.
Recall that both 
and 
are cyclic
quadrilaterals, and so
and 
Now we can combine this with our previous result and we have that
Therefore, 
, 
, 
are
collinerar. Q.E.D.
Furthermore, the converse is also true. That is, if the feet of the
perpendiculars dropped from a point 
to the sides of
the triangle are collinear, then 
is on the
circumcircle.
Proof: Left to reader as an exercise!