Bouncing
Barney
By
Gayle Gilbert
Barney is in the triangular room shown here. He walks from a point on BC parallel to AC. When he reaches AB, he turns and walks parallel to BC. When he reaches AC, he turns and walks parallel to AB.
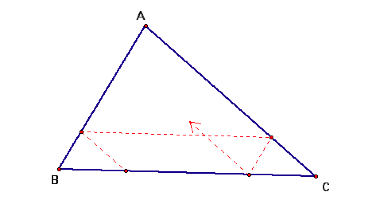
I will prove that Barney eventually return to his original starting point.
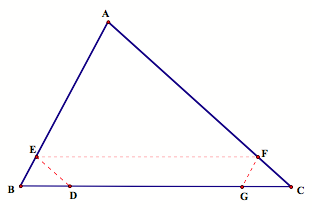
Let Barney start at some point D on BC. He then walks parallel to AC until he
reaches AB at point E. He then
walks parallel to BC until he reaches AC at point F. Then Barney walks parallel to AB until he reaches point G on
BC. Now we have parallelograms
BEFG and DEFC. Therefore, 
, 
, and 
, so by AAS, 
.
Now, Barney walks from point G parallel to AC until he reaches AB at point H, then he walks parallel to BC until he reaches AC at point I.
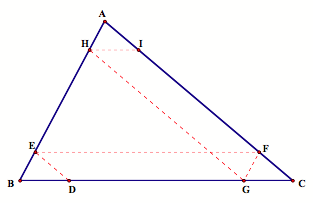
Now, we have parallelograms AFGH and CGHI since opposite
sides are parallel. Thus, 
, 
,
and 
,
so 
by AAS. Since 
and 
, then 
by the
commutative property. Therefore, 
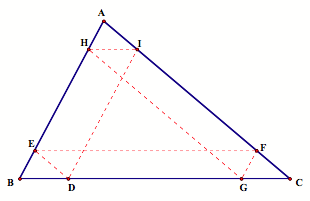
and 
, so quadrilateral AIED must be a parallelogram. Thus, Barney ends in the same place he
started and hit the wall in 6 places.
Click here to use a script tool of Bouncing Barney.
Notice that the distance Barney travels is the same as the
perimeter of the triangle. The
perimeter of 
The
distance traveled by Barney is 
by substitution
because opposite sides of parallelograms are equal. Since we have similar triangles, DE=CF, FG=AH,
and HI=BD. Therefore, we can substitute and
rearrange again, since addition is commutative, and we have the distance traveled
by Barney is equal to the perimeter of the triangle.
What if Barney had started at the midpoint of BC? In this case, Barney would have only hit the walls 3 times (once at the midpoint of each wall).
This is because 
. Here, Barney
travels a distance of half the perimeter.
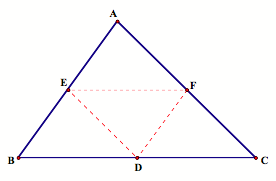
What if Barney had started on line BC outside of the walls? In this case, Barney still hits the ÒwallsÓ 6 times. Click here for a script tool of external Bouncing Barney. For still we have parallelograms and congruent triangles.
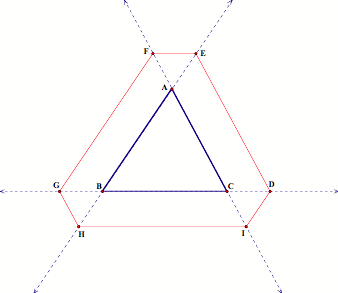
By using parallelograms and congruent triangles, we can again see that Barney ends at his same starting point.
What would happen if we were to start somewhere in the interior of the room? Well, we would still hit the wall six times:
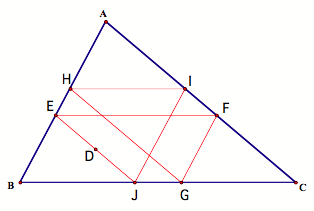
What would happen if we started at the centroid of the triangular room? Well, just like if we started on a midpoint, we hit the wall two times before returning to our original destination:
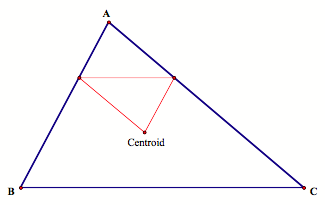
Notice that we have congruent triangles (the red triangle and the top small triangle), and if we were to continue our lines we would have nine congruent triangles. Thus, we can see that the point at which Barney will hit the wall if he starts at the centroid is the trisection point of the walls.
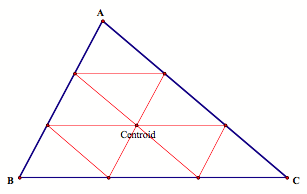
If Barney starts at the centroid, then notice that this is
the intersection point of the walking path if he had started at a trisection
point of one of the walls. So he
only travels one third of the distance, which is one third of the
perimeter.