CevaŐs
Theorem
By
Gayle Gilbert
Consider 
. Select a point
P inside the circle and draw lines AP, BP, and CP extended to their
intersections with the opposite sides in points D, E, and F respectively.
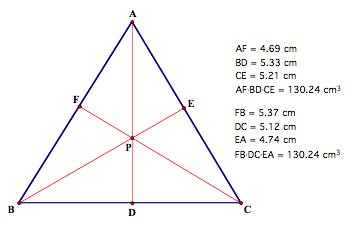
Notice how (AF)(BD)(CE)=(FB)(DC)(EA). Click here for a GSP script tool.
We will prove that 
for any
triangle.
LetŐs construct a line through B parallel to AD and line CF, and letŐs call the intersection point X. Now, letŐs construct a line through C parallel to AD and line BE, and letŐs call the intersection point Y.
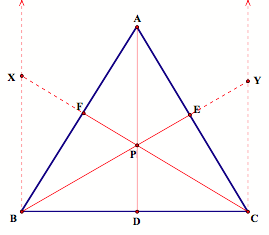
By vertical angles, 
, and by the Z-principle, 
. Therefore, 
. Thus, 
.
Likewise, 
. Thus, 
.
since 
(shared in both
triangles) and 
(corresponding angles). Thus, 
.
Likewise, 
. Thus, 
.
Now, letŐs multiply these three equations together:
Conversely, letŐs suppose
that D, E, and F are points on BC, AC, and AB respectively and satisfying
Let Q be the intersection point of AD and BE, and let FŐ be the
intersection point of CQ and
AB. Since AD, BE, and CFŐ are
concurrent, then we have
When we combine our
equations, we have
Therefore, AD, BE, and CF are concurrent.
QED.
Note: Since we know CevaŐs Theorem must be satisfied for any concurrent point, then we can use this theorem to prove the concurrency of medians (if P is the centroid), the lines of the altitudes (if P is the orthocenter), the bisectors of the angles (if P is the incenter), the perpendicular bisectors of the sides (if P is the circumcenter), or any other special concurrency points. If we can prove that CevaŐs Theorem is satisfied with any of these special points, then we can prove that the points are indeed concurrent.