Untitled Document

Constructions and a Conic

Instructional Unit

Synopsis: This is a set of materials designed to give secondary students an in-depth look at geometric constructions and parabolas. The materials include GSP constructions, Maple worksheets, graphing calculator files, and movie files.

Pre-requisites: The students need to have familiarity with parabolas and geometric constructions.

Caveat: Depending on the students' familiarity with constructions, the instructor may wish to make explicit the fundamental assumptions associated with restricting oneself to the use of an unmarked straightedge and a self-collapsing compass. GSP's graphical inerface nicely embeds these assumptions, and so they may be largely left implicit if the bulk of the work is done through the computer.

The lesson begins with a deceptively simple question:

Question: We know that a parabola whose directrix is parallel to the x-axis can be written in the form

When we initially learn about parabolas and the equations for their graphs, we are often taught (rather casually) how the parameters a and c affect the graph. Rarely is the role of the parameter b mentioned. Now, watch this movie file of a parabola, animated so that the parameter b changes. The question is this: What is the locus of points traced by the vertex of this parabola (allowing b to range from -∞ to ∞)?

Suggested lesson development: Using GSP, help the students get a sense of what this might look like by tracing the entire movement of the parabola, as here. The students might very naturally wish to see only the locus of points created by the movement of the vertex. Ask them: How might we get GSP to trace just the locus of points of the vertex? (That would require constructing the vertex of the parabola from a finite number of points on the parabola.) This leads to a very interesting sub-question, which may be pursued, depending on the allotment of time and the mathematical sophistication of the students. Sub-question 1: Given the graph of a parabola whose directrix is parallel to the x-axis, is it possible to explicitly construct the vertex of the parabola? A set of materials for those interested in pursuing this question may be found here.

To pursue this question, it may be beneficial for the students to rewrite the equation of the parabola into a form where the coordinates of the vertex are more explicit. Lead them to:

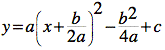
Ask the student's how the vertex will move as the value for b varies? Help them to understand that the vertex moves in the y direction at the square of the rate that it moves in the x direction. What kind of graph has that motion? A parabola of course! The following applet lets you see this visually, simply drag the point labeled 'b' to vary the value of b in the equation of the parabola. You may clear the trace by clicking the X in the bottom right-hand corner. (To find out how to create workarounds for Java sketchpad, including the one used in this applet to plot the vertex, click here.)

Sorry, this page requires a Java-compatible web browser.

Sub-question 3: What is the equation for this new parabola? A Maple worksheet (save the link's target locally, and then open, or you may just get a jumble of text) has been prepared that may be of assistance in guiding students to a solution. It may need modification depending on the familiarity the students have with Maple.

What do I, as a teacher, do with all this material?

I realize that all of these Maple worksheets, GSP worksheets, and Java applets hardly constitute some hard and fast lesson plans. How this material is used with specific students depends very much on the circumstances and idiosyncracies of those students and their teacher. Were I to utilize this material in a mathematics classroom, I would most likely proceed as follows:

1) I would situate the lesson as problem-based learning. That is, I would approach the students with the initial question (what is the locus of ...) and we, as a class, would attempt to formulate a sensible answer. It is likely that the students would need some initial direction, and so I would direct them to the movie file, where they can watch the whole parabola move without any of its points tracing, and ask them to formulate an initial conjecture for the locus. As a class, we would record the consensual hypotheses. I would then ask them how we might demonstrate which, if any, of our hypotheses was correct? Following this question, I would provide them with time to experiment with GSP (if this were available). I would ask them how we can get GSP to draw a general parabola for us? This could lead nicely into 2 parallel paths: the geometric definition of a parabola, or an algebraic attempt to plot a function with parameters specified. Either way, we'd be well on our way.

After we had successfully figured out how to draw a parabola (note the we, not that I would just come out and tell them a way), I would show them the trace feature and the GSP sketch with the entire parabola in 'trace' mode, while 'b' is animated. Time should be given afterwards for some group reflection on our conjectures, given this new evidence. The question should naturally arise, can we just trace the vertex? Depending on whether the students had chosen the geometric or algebraic path (or both), I'd then broach the question of how we can plot the vertex. For the geometers, this leads to sub-questions 1 and 2 (for more advanced students). For the algebraists, this leads to some nice calculation (for which I've provided another Maple worksheet - again, save it locally and then open - but I'd ask them to write an algorithm before allowing them to use Maple to help with the calculations). In either case, after they had determined that (and how) we can plot the vertex, I'd explain to the geometers the underlying GSP difficulty with actually carrying it out, but I'd let them play with the applet above.

Now, it is safe to assume that most of the students will resolve that the locus is a parabola, and so we can begin to explore sub-question 3. The Maple worksheet can carry out the calculations for them, but the real fun is having them decide what calculations should be done. Thus, I'd ask them to write another algorithm for computing this formula, and then use the Maple worksheet (or write another, depending on their algorithm) to carry out the computations.

I anticipate that this whole process takes several days. What is the benefit of spending so much time on a single question? I believe there are many, but I mention only a couple here: 1) This process models the behavior of mathematicians - an interesting problem is posed, and lots of mathematics is learned in the process of solving it. 2) While not every set of students will follow the flow I've described above, and varying levels of intervention will be necessary, my (albeit limited) experience tells me that mathematics seems less arbitrary when it comes from within. That is, the students will be posing most of the intermediate questions and results as they follow their own thinking, rather than attempting to imagine the logic behing the train of thought their teaching imposes upon them.

Feel free to use any of the material that you find helpful, and to disregard any that you don't. A .zip file can be downloaded here, which contains all the relevant materials in one location. At least an introductory knowledge of GSP and Maple would be very beneficial, and probably necessary. GSP will create the Java sketches for you, but there are several caveats, so be sure to visit the link to the workarounds I provided earlier.