The Department of Mathematics and Science Education Allyson Hallman
Explorations with Sine and Cosine
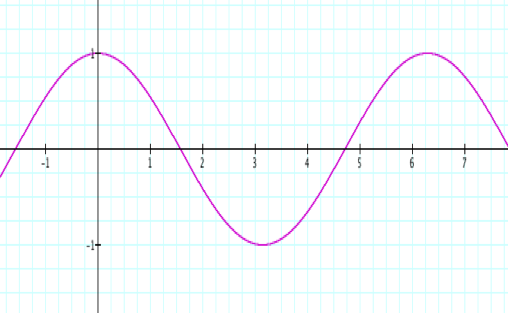
Consider the graphs of:
It is easy to see that the sine graph is actually the cosine graph shifted horizontally to the right by units. Also, the maximum value and minimum value for both graphs is 1 and -1, respectively.
What kind of transformations on these graphs can we produce?
Part I: Multiply the functions by a constant a. What effect will this have on our graphs?
So we shall consider the following two graphs where values for a range from -5 to 5. Clicking on the graphs below will illustrate the affect of varying values of a. A second graph is included that has a = 1 so that this graph may be compared with the graph where a varies.
We have learned: Multiplying our function by a constant affects the amplitude of each graph. Amplitude refers to the half the absolute value of difference between value of the maximum and minimum. The absolute value of a is the amplitude of the curve. We know that y = sin x and y = cos x have the same minimum and maximum values of -1 and 1, respectively (remember your unit circle). So the amplitude of these is 1. Notice that when a is negative, not only is the amplitude affected, but also, the graph is reflected over the x-axis. We should certainly expect this from our previous knowledge of transformations of functions. (We know that –f(x) reflects our graph over the x-axis.) Also, take note that the zeros of the sine and cosine functions do not change for varying values of a.
Part II: Multiply the functions’ x-variable by a constant b. What effect will this have on our graphs?
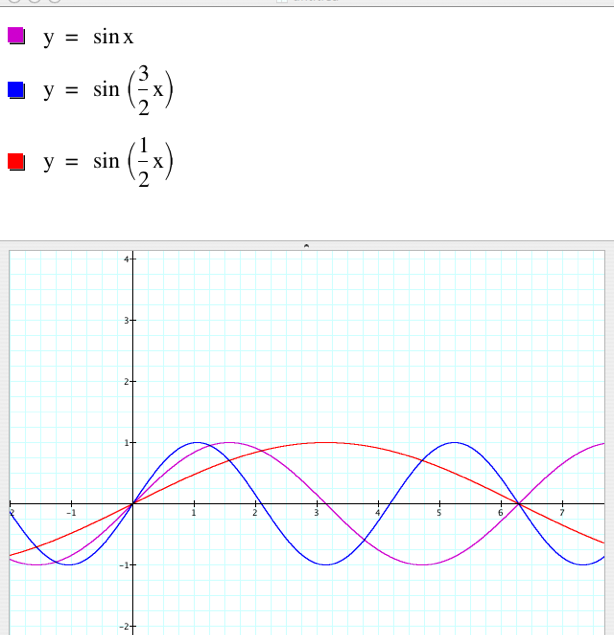
So we shall consider the following two graphs where values for b range from 0.25 to 2. Clicking on the graphs below will illustrate the affect of varying values of b. Pictured below, b =1. Clicking these graphs will vary the values of b.
We have learned: Multiplying the input of our function by a constant affects the period of the each graph. The period of the graph is the distance required to progress through one complete “wave” of the sine graph (also called wavelength for you physics nuts). We can say the period is the distance between corresponding points on the curve. For example the distance between the consecutive peaks on the curve. We know from our work earlier with amplitude that maximum value of the sine and cosine graph is 1. We also know that and . The next input which produces a value of 1 is for sine and 2p for cosine. Thus the period for sine is and for cosine . The period of both the sine and cosine graph is 2p. To understand more closely the affect of b on the period of the sine and cosine graph let’s consider two specific cases:
Using our purple graphs above as a base line, we can see that if b > 1 (the blue graphs), our period decreases and if b < 1 (the red graphs) the period increases.
Restrict the domain of y = sin x and y = cos x to [0, 2p] which produces one complete period. So taking into account multiplying our input by b, we have . Then dividing all sides by b, we have .
Thus, the period of sine and cosine graphs is .
Part III: Add a constant, c, to the input of our function. What effect will this have on our graphs?
So we shall consider the following two graphs where values for c range from -5 to 5. Clicking on the graphs below will illustrate the affect of varying values of c. A second graph is included that has c = 1 so that this graph may be compared with the graph where c varies.
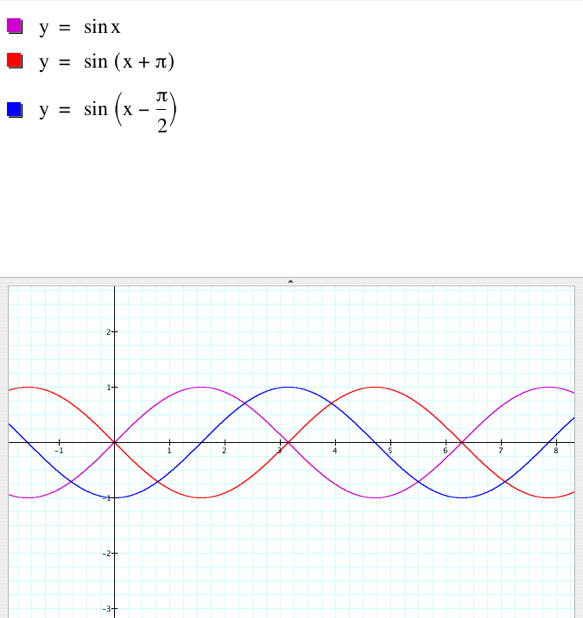
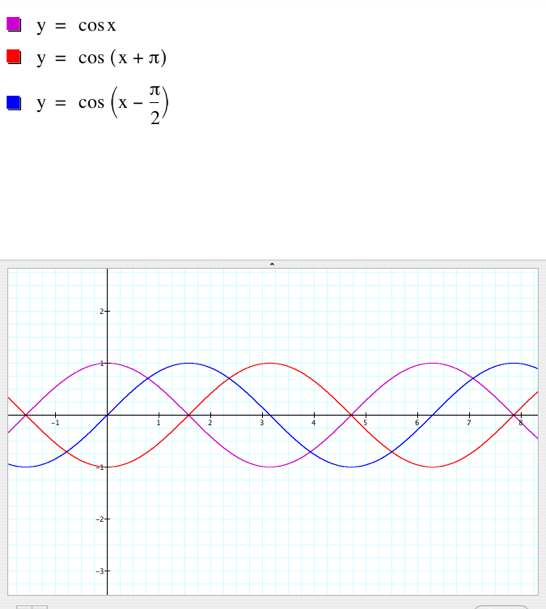
We have learned: This is really quite unsurprising. We know from our work with transformations that f (x + c) produces a horizontal shift; the graph shifts left (red graphs) if c > 0 and right (blue graphs) if c < 0, as we can see below.
There is some “coolness” going on here. Sine and cosine are periodic functions and the period of each is 2p. So adding the period, or multiples of the period, to the input will shift the graph so that it is identical to the original graph of y = cos x or y = sin x. Not convinced? Check this out exploration in graphing calculator: If you vary the value of n manually by moving the dot on the bar (don’t press play, it moves too fast) you can see the shifts for all multiples of p from -6 to 6. Notice that for all even values of n (all multiples of 2p) the graph is identical to the original parent function y = cos x. Also, as mentioned earlier, the sine graph is simply the cosine graph shifted units to the right and conversely, the cosine graph is just the sine graph shifted units to the left. In fact this holds true for multiple of 2p that is added to . CLICK ON THE EQUATIONS BELOW to explore these relationships in graphing calculator. Again, if you vary the value of n manually by moving the dot on the bar (don’t press play, it moves too fast) you can see the shifts for all multiples of p from -10 to 10. Notice that for all even values of n (all multiples of 2p) the sin graph becomes identical to graph is identical to the cosine graph and vice versa. and
Things also become more interesting if we consider b and c simultaneously. and
For example, y = sin (2x + p) we would expect that sin graph would be shifted by p, but as we can from the graphs below, y = sin (2x + p) is not shift by p. In fact it is shifted by . Why of course, p is not added directly to x. It is added to 2x, so to consider what constant is added to x we must factor our the coefficient of x.
y = sin (2x + p)				y = sin (x + p)
Tying it all together: A little conclusion
= Amplitude
= Period
= horizontal or phase shift.
Some Special Phase Shifts:
, where k is an integer.			, where k is an integer.
Go home?