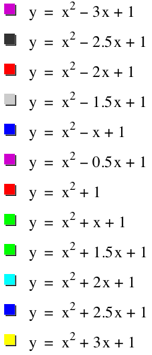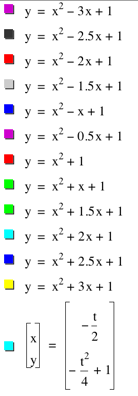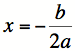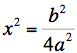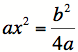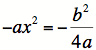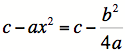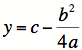Department of Mathematics and Science Education

 

Allyson Hallman

 

 

 

 

A detailed examination of ÒbÓ

 

 

 

Consider:

 

 

 

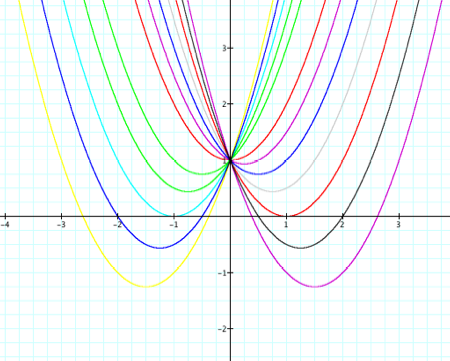
What effect does b have? LetÕs consider the case where a = 1 and c = 1.

 

 

 

Graph:

 

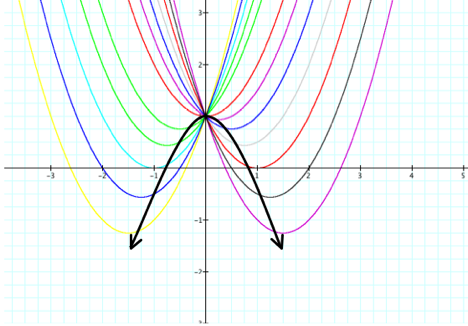
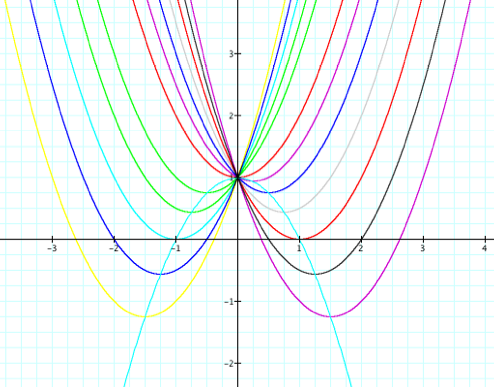
We can classify all the pretty graphs into one of the three following categories:

 

 

 

 or

2 roots

1 root

No real roots

 

 

 

ItÕs all about the discriminant: b2 - 4ac

To have two real roots the discriminant must be greater than 0.

To have one real root the discriminant must be equal to 0.

To have no real roots the discriminant must be less than 0.

 

And we know a and c are 1. Substitution gives us:

 

 

 

 

 

 

 

b < -2 or b > 2

b = -2 or b = 2

b > -2 and b < 2

 

 

 

What else interesting might we find in the graph?

 

 

It seems that connecting the vertices of each parabola generates yet another parabola.

 

(I sketched this one in Òpaint and copied it on top of my graphs.)

 

 

 

 

 

Can we somehow generalize this parabola, based on b?

Sure, what are the vertices of   for all values of b.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

We can conclude the vertex of  is

WouldnÕt it be great to graph this? Ah, how about parametric equations.

 

 

 

Can we find a function to represent this parametric equation.

 

 

 

We can start with:

 

 

 

We know the vertex of the parabola is (0, 1). So we have:

 

 

 

It only remains to find a. We can do this by plugging in a point on the parabola for (x, y) and solving the resulting equation for a. For ease of calculation we will choose (-1, 0) which is generated by plugging in

t = 2 to our parametric equations for x and y.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Which simplified gives us  as the equation that generates all the vertices of all the parabolas of the form .

 

 

 

Now, the really fun partÉ.. Can we find an equation that generates the vertices of when a, b, and c vary?

 

 

 

Generally, what is the form of the vertex of ?

 

 

 

Completing the square, we have:

 

 

 

 

 

 

 

 

 

Ah, so in general the vertex of   is 

 

So we have these two parametric equations:  and  

Can we write one in terms of the other and so generate a general equation for the vertices of ?

 

 

The x-coordinate of the vertex of a parabola.

 

 

Square both sides.

 

 

Multiply both sides by a.

 

 

Multiply both sides by -1.

 

 

Add c to both sides.

 

 

Substitute  what we calculated as the y-coordinate of our vertex.

 

 

BIG CONCLUSION

(drum roll pleaseÉ.)

 

And so at last the equation   generates all the vertices of the parabolas of the form .

 

 

Go Home?